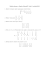Test wielokrotnego wyboru z matematyki - Funkcje

Test wielokrotnego wyboru z matematyki - Funkcje trygonometryczne.
Nr.
1.
Tre±¢ zadania
Wiadomo, »e
a)
wtedy
b)
wtedy
c)
wtedy
2.
cos x =
3
5 i
Wyra»enie
tg 41◦ tg 42◦ tg 43◦ . . . tg 49◦
jest równe 2
b)
jest równe 1
c)
jest liczba niewymiern¡
Dana jest funkcja
a)
Dziedzin¡ funkcji
b)
Dziedzin¡ funkcji
c)
Dziedzin¡ funkcji
4.
a)
b)
c)
5.
Wyra»enie
Wyra»enie
a)
1
tg2 x
tg2 2x
√
f (x) = 1 − 2 cos x.
π
5π
jest x ∈ h 3 + 2kπ, 3 + 2kπi k ∈ Z
π
5π
jest x ∈ ( 3 + 2kπ, 3 + 2kπ) k ∈ Z
5π
1π
jest x ∈ h− 3 + 2kπ, − 3 + 2kπi k ∈ Z
sin x
sin x
+
1 + cos x 1 − cos x
po uproszczeniu jest równe
cos2 2x − 1
sin2 2x − 1
po uproszczeniu jest równe
b)
| sin 5x| ≤
π
π
kπ
x ∈ h− 30
+ kπ
,
+
i
k
∈
Z
5 30
5
π
kπ 7π
kπ
x ∈ h 6 + 5 , 30 + 5 i k ∈ Z
c)
pusty
6.
a)
7.
Rozwi¡zaniem nierówno±ci
Dane jest równanie
1
2 jest zbiór
| sin x| = sin x + 2.
W takim razie
a)
równanie to ma niesko«czon¡ ilo±¢ rozwiaza«
b)
rozwi¡zanie rownania jest zbiór pusty
c)
rozwi¡zaniem tego równania jest
8.
x = 32 π + 2kπ
sin x
< 1. Zatem
| sin x|
x ∈ (π + 2kπ, 2π + 2kπ) k ∈ C jest
x ∈ hπ + 2kπ, 2π + 2kπi k ∈ C jest
zbiór
b)
zbiór
c)
zbiór pusty jest rozwi¡zaniem tej nierówno±ci
...
...
...
...
...
...
....
....
....
. ..
. ..
. ..
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
Rozwi¡zaniem nierówno±ci
ctg2 x > 1
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
rozwi¡zaniem tej nierowno±ci
jest
zbior pusty
b)
x ∈ (kπ, π4 + kπ) ∪ ( 3π
4 + kπ, π + kπ) k ∈ Z
x ∈ (2kπ, π4 + 2kπ) ∪ ( 3π
4 + 2kπ, π + 2kπ) k ∈ Z
10.
......
......
......
rozwi¡zaniem tej nierowno±ci
a)
c)
Punkty
...
...
...
k∈C
Dana jest nierówno±¢
a)
9.
Nie
...
...
...
4
sin x
2
sin x
1
sin 2x
b)
c)
2
Tak
sin x = 45
ctg x = 34
tg x = 34
a)
3.
x ∈ 0,
π
Przygotowaªa Klaudia Wrzask
f (x) = 2 sin x2 + 3 sin x3 . Zatem
podstawowym funkcji jest T = 6π
podstawowym funkcji jest T = 4π
podstawowym funkcji jest T = 12π
Dana jest funkcja
a)
okresem
b)
okresem
c)
okresem