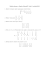Symulacja handlu pozwoleniami na emisje z

SYMULACJA HANDLU POZWOLENIAMI NA EMISJE Z WYKORZYSTANIEM
MODELU DLA SYSTEMU WIELOAGENTOWEGO
JAROSŁAW STACZAK
Instytut Bada Systemowych PAN
Streszczenie
W pracy tej opisano model handlu pozwoleniami na emisj CO2 lub innymi
podobnymi towarami, uwzgldniajcy niektóre aspekty rzeczywistych rynków
i zawieranych tam transakcji, moliwy do zastosowania w systemie wieloagentowym
lub innym zblionym rodowisku symulacyjnym np. ewolucyjnym (jako przykład tzw.
Agent-Based Computational Economics – ACE). Opisywany model powstał na
podstawie danych, analogii i pomysłów zwizanych z symulacjami rynku pozwole
na emisj CO2 zawartego jako wynik porozumie z Kioto, dlatego te w pracy tej
znajdzie si duo odniesie do modeli tego rynku. Praca niniejsza opisuje równie
now, rozszerzon, dynamiczn metod opisu działania takiego rynku, w której
uwzgldniono wpływ cen zakupu pozwole na decyzje kupna oraz moliwo
negocjacji cen pozwole przez kontrahentów.
Słowa kluczowe: handel pozwoleniami na emisj, Protokół z Kioto, algorytm ewolucyjny
1. Wprowadzenie
Wystpujca od pewnego czasu tendencja do niestabilnoci i ocieplania si klimatu skłoniła
wielu badaczy do zajcia si tym tematem. Wród wielu z nich panuje opinia, która obarcza win
za to zjawisko emisj gazów powstajc w wyniku spalania paliw kopalnych, a w szczególnoci
emisj CO2. W zwizku z tym postanowiono zmniejsza jej poziom, a jedn z przyjtych metod
ograniczania jest przydzielenie limitów emisji krajom oraz ewentualny handel tymi pozwoleniami
na emisj. O ile niektóre kraje bd mogły stosunkowo tanio zmniejszy poziom swoich emisji
poniej przyznanych limitów, o tyle inne bd wolały zapłaci za powikszenie emisji poza
przyznany im limit. Alternatyw dla kupowania pozwole od innych krajów jest oczywicie
ograniczanie własnej emisji przez wdraanie nowoczeniejszych technologii i uycie innych
sposobów pozyskiwania energii ni spalanie paliw. Znaczna cz krajów rozwinitych
zobowizała si przestrzega nałoonych limitów podpisujc konwencj zwan protokołem
z Kioto.
W artykule rozpatrywany jest problem handlu pozwoleniami na emisj z uwzgldnieniem
negocjowanych cen zakupu/sprzeday i ich wpływu na otrzymane rozwizania. Skonstruowano
model takiego rynku, w którym uwzgldniony jest wpływ cen zakupu pozwole na funkcj celu
zadania, a przez to na decyzje o zakupie bd nie pozwole. Dodatkowo powstała te wersja
rynku, w którym kady uczestniczcy podmiot optymalizuje swoj prywatn funkcj celu. Jest to
zreszt sytuacja zgodna z tym, co obserwuje si w typowych transakcjach wolnorynkowych.
Jarosław Staczak
Symulacja handlu pozwoleniami na emisje z wykorzystaniem
modelu dla systemu wieloagentowego
171
2. Opis problemu
Aby w pełni zrozumie, jak tego typu zobowizania wpływaj na gospodark oraz jakimi
prawami rzdzi si taki rynek, badacze staraj si budowa jego modele i znale optymalne
rozwizania, pozwalajce przewidzie ceny pozwole, oraz koszty ograniczania emisji dla
rónych krajów [6]. Istotn spraw jest te zbudowanie modelu samego przeprowadzania
transakcji oraz rozwizanie wielu innych problemów, zwizanych np. z dokładnoci
raportowanych przez kraje poziomów emisji itp. [2, 3, 7, 9,].
W statycznym modelu handlu pozwoleniami na emisj CO2 przyjmuje si, e transakcje zachodz
tylko w punkcie równowagi rynku po cenach równych kracowym kosztom w tym punkcie,
jednakowym dla wszystkich uczestników rynku. W proponowanych modelach dynamicznych handlu,
teoretyczne wartoci cen mog by okrelane przez model, jako pochodne kosztów redukcji dla danego
poziomu emisji, lecz nie s one uwzgldniane w stosowanej funkcji celu problemu, dziki której
staramy si znale punkt cen równowagi i wynikajce z niego koszty redukcji emisji oraz zakupu
pozwole. W rozpatrywanych wczeniej modelach nie ma te mowy o ewentualnym negocjowaniu cen
lub dodatkowych kosztach zawarcia transakcji np. typu prowizji dla poredniczcych agencji lub
podobnych. Model ten zakłada właciwie przymus przeprowadzenia odpowiednich transakcji, jeeli
tylko wystpuje midzy kontrahentami rónica kosztów kracowych, a rozwizanie optymalne znajduje
si w punkcie równowagi [6]. Ostatecznie liczy si bilans zakupów i przyjmuje si cen równ kosztom
kracowym w punkcie równowagi. Znane s wobec tego jedynie ceny kocowe, bez wnikania w to,
w jaki sposób rynek do nich doszedł. Takie postawienie problemu jest do odległe od realiów
rzeczywistego rynku. W zwizku z tym opracowano nieco bardziej skomplikowany model tego rynku
zaprezentowany w tej pracy, w którym uzupełniono brakujce elementy o moliwo negocjacji cen i o
wpływ rzeczywistych wartoci cen zawieranych transakcji na posta otrzymywanych rozwiza. Cały
rynek rozpatrywany jest dynamicznie, jako szereg transakcji zachodzcych w rónych chwilach
czasowych. Dla kadej potencjalnej transakcji mona policzy wartoci cen teoretycznych i na ich
podstawie prowadzi negocjacje i ustala cen, po której zachodzi transakcja.
3. Modele statyczny i dynamiczny rynku pozwoleĔ
Idea handlu pozwoleniami opiera si na załoeniu, e pewne kraje mog taniej zredukowa
emisj i wtedy maj nadwyk niewykorzystanych pozwole na emisj. Mog je wobec tego
odsprzeda krajom, które ze wzgldu na koszty wol emitowa wicej, ni im na to pozwalaj
limity, jak na przykład te, które s narzucone przez protokół z Kioto.
Sytuacja taka jest opłacalna wtedy, jeli cena sprzedawanych pozwole na emisj bdzie
nisza ni koszt kracowy redukcji emisji w danym kraju. Moe si zdarzy, e krajowi
sprzedajcemu bdzie si opłacało redukowa emisj własnymi rodkami, jeli koszt kracowy
redukcji jest niszy ni moliwa do uzyskania cena za pozwolenia, a uzyskane w ten sposób
niewykorzystane pozwolenia sprzedawa. Sytuacj t ilustruj rysunki 1 i 2.
172
POLSKIE STOWARZYSZENIE ZARZDZANIA WIEDZ
Seria: Studia i Materiały, nr 33, 2010
Rys. 1. Koszty redukcji emisji CO2 bez handlu
(Qi) oraz z handlem (Qk) dla kraju kupujcego
Rys. 2. Koszty redukcji emisji CO2 bez handlu
wynosz 0, a z handlem Qk dla kraju
sprzedajcego,
Ki – ograniczenie emisji (pozwolenia na
emisj) wynikajce z protokołu w Kioto, Fk –
emisja po zakupie dodatkowych pozwole, F0
– emisja pocztkowa.
Ki – ograniczenie emisji (pozwolenia na
emisje) wynikajce z protokołu w Kioto, Fk –
emisja po sprzeday czci pozwole, F0 –
emisja pocztkowa.
Koszty kracowe (tzw. shadow price) s definiowane jako pochodne kosztów w danym
punkcie. Jednake na cen kupowanego dobra wpływ ma najczciej duo wicej czynników
natury ekonomicznej, politycznej i innych. Dlatego te w opisywanym rozwizaniu przyjto
załoenie, e transakcja dochodzi do skutku, jeli wynegocjowana cena pozwolenia jest nisza od
kracowego kosztu redukcji strony kupujcej, a wysza od kracowego kosztu redukcji strony
sprzedajcej. Aby unikn modelowania samego procesu negocjacji, cena transakcji jest losowana
z odpowiedniego przedziału cenowego, z maksimum prawdopodobiestwa wylosowania ceny
redniej.
W zaproponowanym modelu dokonano pewnych istotnych zmian w stosunku do wersji
podstawowej przedstawionej np. w pracy [6] (w opisywanym u modelu nie s brane pod uwag
niepewnoci emisji). Najistotniejsz jest zmiana funkcji celu. We wczeniejszych modelach funkcja
celu (1) i ograniczenia (2–3) wygldaj nastpujco:
n
F = min ¦ Ci ( xi )
xi i =1
xi ≤ K i + si
(1)
(2)
n
¦ si = 0
(3)
i =1
gdzie Ci(xi) – koszty redukcji emisji do wartoci xi dla kraju i; si – całkowita liczba
zakupionych pozwole przez kraj i, Ki – limit na emisj CO2 wynikajcy z protokołu podpisanego
w Kioto; xi – emisja kraju i; n –liczba krajów biorcych udział w rynku.
Tak wic minimalizujemy koszty redukcji emisji do załoonego poziomu dla całego rynku.
Kady uczestnik nie moe przekroczy limitu narzuconego przez protokół z Kioto, ewentualnie
powikszonego o liczb zakupionych pozwole na emisj lub zmniejszonego o liczb sprzedanych
pozwole.
Jarosław Staczak
Symulacja handlu pozwoleniami na emisje z wykorzystaniem
modelu dla systemu wieloagentowego
173
W nowym modelu funkcja celu ma posta (4) z ograniczeniami (5–9):
T
G=
n
(C i ( x j−1, i ) − (Ci ( x ji ) − s ji ⋅ π ji ))
¦ max
¦ smax
x
π
j =1
ji
i =1
ji
(4)
ji
T
xTi ≤ K i + ¦ s ji
(5)
j =1
n T
¦ ¦ s ji
(6)
=0
i =1 j =1
(7)
0 ≤ s ji ≤ s max
­π
¯0
π ji = ®
uczestnicy transakcji j
ji
pozostali
­ 0
°
s ji = ® − s ji
° s ji
¯
bez udzialu w transakcji j
sprzeda w transakcji j
(8)
(9)
zakup w transakcji j
gdzie G –warto globalnej maksymalnej redukcji kosztów obnienia emisji; T – liczba
zawartych transakcji; Ci(xji) – koszty zmniejszenia emisji dla podmiotu i od wartoci pocztkowej
F0i do xji po j transakcjach; Ki – narzucone przez protokół z Kioto ograniczenie emisji dla
podmiotu i; n – liczba uczestników rynku; xji – emisja podmiotu i po j transakcjach; sji – liczba
pozwole zakupionych przez podmiot i w transakcji j; smax – maksymalna liczba pozwole, któr
mona sprzeda/kupi w jednej transakcji; πji – cena pozwole kupionych/sprzedanych przez
podmiot i w transakcji j.
Wystpuje w niej maksymalizacja rónicy midzy tym, co byłoby wydane na redukcj emisji bez
handlu pozwoleniami, a tym, co wydawane jest z uwzgldnieniem handlu po kadej transakcji.
Optymalizacja przeprowadzana jest take na potrzeby kadej transakcji. Umoliwia to uwzgldnienie
ceny w rozliczeniach kosztu zakupu i sprzeday pozwole co ma znaczny wpływ na opłacalno
transakcji i decyzj, czy warto kupi/sprzeda, czy te warto inwestowa własne rodki na ograniczenie
emisji. Dziki nowej funkcji celu staramy si znale rozwizanie, które maksymalizuje rónic,
midzy kosztami bez handlu, a kosztami z handlem pozwoleniami, czyli innymi słowy staramy si
maksymalizowa zysk na handlu pozwoleniami. W poprzedniej funkcji celu minimalizowano koszty
redukcji emisji, bez jakiegokolwiek uwzgldniania cen zakupu i sum przeznaczanych na ten cel,
a koszty te mog by znaczne i porównywalne z tymi, które wydawane s na samodzieln redukcj
CO2. Model zakłada równie nieco zmodyfikowan metod ustalania cen pozwole. Modyfikacja
polega na tym, e ustala si pewn cen minimaln, poniej której cena pozwolenia nie spada.
Przeciwdziała to sytuacji, w której kraj majcy emisj poniej wartoci ustalonej protokołem z Kioto
ma zerowe ceny kosztów redukcji emisji i w zasadzie mógłby rozdawa pozwolenia za darmo (taka
sytuacja ma miejsce w testowanych przykładach dla krajów byłego ZSRR, ilustruje to Rys. 2).
Właciwa cena, po jakiej nastpuje zakup pozwolenia, oraz ich liczba, podlegaj negocjacjom
i właciwie nie mog by znane przed komputerow symulacj działania rynku. W zwizku z tym
potrzebny jest model symulacji prowadzonych negocjacji. W pracy przyjto statyczny model losowania
odpowiednich wartoci. Liczba sprzedawanych w kadej transakcji pozwole jest losowana z pewnego
przedziału wartoci. Podobnie cena pozwole jest losowana jako warto z przedziału pomidzy
kosztem kracowym kupujcego (cen maksymaln), a kosztem kracowym sprzedajcego –
ewentualnie zmodyfikowanym (cen minimaln). Wykorzystany do tego celu jest odpowiednio
174
POLSKIE STOWARZYSZENIE ZARZDZANIA WIEDZ
Seria: Studia i Materiały, nr 33, 2010
zmodyfikowany (przycity) rozkład normalny, z wartoci oczekiwan równ redniej cen
teoretycznych kontrahentów (warto redni mona zmienia, co moe symulowa wiksz lub
mniejsz sił w negocjacjach jednej ze stron). W przyszłych badaniach przewiduje si zbadanie innych
sposobów symulowania negocjacji. Przedstawiony powyej model równie nie umoliwia jednak
niezalenego potraktowania wszystkich podmiotów biorcych udział w rynku. W dalszym cigu
wszystkie transakcje wrzucane s do jednej formuły (4), która umoliwia znalezienie globalnego
punktu równowagi rynku, okrelenie przepływów rodków finansowych i liczby pozwole, ale nie
ocenia osigni pojedynczych podmiotów, czyli brak jest w nim indywidualnego podejcia do
kadego uczestnika rynku. Moliwe jest jednak rozbicie tego wzoru na poszczególnych uczestników
i zastosowanie go w systemie, w którym kady uczestnik bdzie działa na swoj rk, czyli w np.
systemie agentowym lub wielokryterialnym algorytmie ewolucyjnym:
T
(
(
Gi = ¦ max C i ( x j −1, i ) − C i ( x ji ) − s ji ⋅ π
j =1 s jiπ ji
ji
))
(10)
gdzie Gi – warto maksymalnej redukcji kosztów obnienia emisji dla kadego podmiotu
i=1...n; pozostałe symbole maj takie samo znaczenie jak we wzorach (4–9) z ograniczeniami
identycznymi jak w modelu jednokryterialnym, czyli wzorami (5–9).
Model dla systemu wieloagentowego nie róni si bardzo od modelu jednokryterialnego.
Jedyn rónic jest rozbicie kryterium globalnego na poszczególne podmioty. Dziki temu kady
podmiot jest oceniany za konkretne swoje osignicia. Jednoczenie naley oczekiwa, e
osignity punkt równowagi rynku nie bdzie znaczco odbiega od wyników osiganych w dwu
wczeniej opisywanych modelach, gdy decydujcy wpływ na ceny i zawierane transakcje maj
takie same funkcje kosztów. Punkt równowagi cen znajdzie si wobec tego w tym samym miejscu,
natomiast znacznie mog si róni osignicia poszczególnych podmiotów, przy braku
uredniajcego działania kryterium globalnego. Potwierdzaj to wyniki uzyskane przy
wykorzystaniu tego modelu wielokryterialn metod ewolucyjn.
4. Algorytmy ewolucyjne uĪyte w symulacjach komputerowych
Do rozwizania postawionych problemów uyto specjalizowanych algorytmów ewolucyjnych
z odpowiednim zakodowaniem problemu i zestawem operatorów. W przypadku symulacji modelu
podstawowego (1) lub nowego z jednym kryterium (4) pojedynczy osobnik zawiera informacje
o wszystkich krajach biorcych udział w rynku, jest wic kompletnym rozwizaniem problemu.
Liczba rynków biorcych udział w symulacji (liczno populacji algorytmu ewolucyjnego) jest
w zasadzie dowolna, oczywicie zbyt dua liczba moe znaczco spowalnia obliczenia.
Symulacja polega na ewolucyjnej modyfikacji i promowaniu rynków o coraz lepszej wartoci
globalnego kryterium jakoci. Algorytm metody przedstawiony jest jako Algorytm 1. Kady kraj
opisany jest danymi, które s takie same, jak w przypadku metody „agentowej” i tam s dokładniej
przedstawione. W metodzie „agentowej” stosuje si podejcie, w którym kady kraj jest
oddzielnym osobnikiem [1, 5], lecz wtedy otrzymujemy jako wynik symulacji tylko jedno
rozwizanie, a wielko populacji jest ograniczona do liczby krajów biorcych udział w handlu –
jest to podejcie, które dobrze nadaje si do symulacji problemu wielokryterialnego i bdzie uyte
przy symulacji takiego modelu. Informacje potrzebne do opisania pojedynczego kraju we
wszystkich rozpatrywanych modelach to:
• cena teoretyczna własnego pozwolenia (shadow price);
• rzeczywista cena aktualnie sprzedanego/kupionego pozwolenia;
Jarosław Staczak
Symulacja handlu pozwoleniami na emisje z wykorzystaniem
modelu dla systemu wieloagentowego
175
• warto zakupionych i sprzedanych pozwole;
• liczba aktualnie zakupionych/sprzedanych pozwole;
• sumaryczna liczba zakupionych/sprzedanych pozwole;
• emisja bieca;
• emisja poprzednia (przed biec transakcj);
• warto biecej i poprzedniej funkcji celu.
S one zawarte w kadym osobniku (agencie) jako odpowiednio liczby całkowite lub
zmiennoprzecinkowe. Do modyfikacji rozwiza słu nastpujce dedykowane operatory
genetyczne. Dla obu wersji symulacji s to:
• przetarg – wylosowany kraj wystawia pewn liczb pozwole na sprzeda, a pozostałe kraje
składaj oferty kupna, wybierana jest najlepsza i tak dochodzi do modyfikacji rozwizania;
• sprzeda bilateralna– wylosowane kraje przeprowadzaj midzy sob transakcje bilateralne,
wymieniajc warunki transakcji, jeli s one opłacalne dla obu stron, transakcja jest
wykonywana.
1.
2.
3.
4.
5.
Inicjalizacja populacji rozwiaza.
Reprodukcja i modyfikacja rozwiza przy uzyciu specjalizowanych operatorów.
Ocena otrzymanycg rozwizan.
Selekcja rozwiza do nastpnego pokolenia.
Jeli nie został spełniony warunek stopu, powrót do punktu 2.
Algorytm 1. Algorytm ewolucyjny w wersji jednokryterialnej
1. Inicjalizacja osobników (agentów).
2. Modyfikacja stanu osobników przy uzyciu specjalizowanych operatorów.
3. Ocena osignitych nowych stanów osobników.
4. Jeli nie został spełniony warunek stopu, powrót do punktu 2.
Algorytm 2. Algorytm metody ewolucyjnej w wersji wielokryterialnej
Operatory te s wykonywane w zalenoci od tego, co wybior podmioty uczestniczce
w handlu. Wybór jest losowy. Właciwe zmienne sterujce problemem to liczba aktualnie
zakupionych/sprzedanych pozwole i wynegocjowana cena transakcji, pozostałe zapamitane
w osobniku dane s potrzebne do przeprowadzenia bilansu rodków i wyliczenia funkcji celu.
Ceny transakcji, jak i liczby pozwole s losowane. Dla liczby pozwole jest to liczba naturalna
z zakresu {1,..,5}, cena pozwolenia jest za losowana jako warto pomidzy cen oferty kupna,
a oferty sprzeday. Symulacja rynku przy pomocy algorytmu ewolucyjnego przeprowadzana jest
etapami, tj. pozwolenia sprzedawane s w niewielkich pakietach, po negocjowanej cenie, dlatego
te zawsze mona dokładnie pozna cen, po której zakupiono pozwolenia. Umoliwia to
prowadzenie dokładnego bilansu wydatków/zysków i ich optymalizacj działania w kadym
kroku. Algorytm tej metody przedstawionjy jest jako Algorytm 2.
176
POLSKIE STOWARZYSZENIE ZARZDZANIA WIEDZ
Seria: Studia i Materiały, nr 33, 2010
5. Wyniki symulacji komputerowych
Symulacje komputerowe przeprowadzono na standardowym zestawie danych, pochodzcych
m.in. z pracy Horabik [8]. Przedstawiaj one dane dotyczce nastpujcych grup krajów: USA,
EU, Japonia, CANZ (Kanada, Australia, Nowa Zelandia), kraje byłego ZSRR (WNP). S to dane
do orientacyjne, m.in. zakładaj udział USA w rynku, cho kraj ten nie podpisał protokołu
z Kioto. Jednake, aby rynek zaczł praktycznie działa trudno jest pomija kraj o najwyszej
emisji CO2. Std najczciej bierze si pod uwag w symulacjach hipotetyczn obecno USA
w rynku handlu pozwoleniami. Natomiast faktyczny brak udziału USA w tym handlu powoduje,
e rzeczywiste ceny pozwole utrzymuj si na duo niszym poziomie ni te z symulacji, gdy
jest zdecydowanie mniejszy popyt na pozwolenia, ni kiedy USA uczestnicz w rynku.
Zakłada si, e koszty redukcji emisji zale kwadratowo od wielkoci redukcji emisji (16),
a ceny pozwole maj warto pochodnej funkcji kosztu dla odpowiedniego poziomu emisji (17).
W tabeli nr 1 zawarte s natomiast odpowiednie współczynniki funkcji (16) i (17).
­°a * ( F0 − F ) 2 dla
C=®
°̄0 dla F ≥ F0
F < F0
(16)
­2 * a * ( F0 − F ) dla F < F0
c=®
¯min dla F ≥ F0
(17)
gdzie a – parametr funkcji kosztu, F0 – emisja pocztkowa, F – emisja bieca, min – minimalna
warto ceny, wprowadzona do oblicze dla urealnienia warunków wyliczania cen.
Tabela 1. Dane wykorzystane do oblicze – współczynniki funkcji kosztów
Kraj
USA
EU
Japonia
CANZ
WNP
Emisja pocztkowa (F0) Parametr funkcji kosztu (a) Limit Kioto (Ki)
MtC/rok
MUSD/(MtC/rok)2
MtC/rok
1820,3
0,2755
1251
1038,0
0,9065
860
350,0
2,4665
258
312,7
1,1080
215
898,6
0,7845
1314
ródło: Horabik (2005).
Dla podejcia tradycyjnego (z załoeniem idealnego rynku) otrzymujemy wynik
przedstawiony w tabeli 2, natomiast przy zastosowaniu obu wersji nowego modelu, wynik
symulacji nie jest pojedynczym zestawem danych, lecz zestawem scenariuszy, gdy warunki jego
otrzymania nie s deterministyczne i nieco róni si w kolejnych symulacjach lub rónych
rozwizaniach tej samej symulacji dla wersji ze standardowym AE. Wynika to nie tylko
z losowego charakteru oblicze ewolucyjnych (zestaw wyników dla zadania tradycyjnego równie
otrzymany był przy uyciu algorytmu ewolucyjnego, wobec czego mog by niewielkie rónice w
rozwizaniach dla wielu symulacji), ale take z zastosowanego modelu negocjacji, w którym cena,
po której zawierana jest transakcja, jest losowana z przedziału, w którym jest ona opłacalna dla
kontrahentów. Ma to modelowa wpływ negocjacji na cały proces handlu.
Jarosław Staczak
Symulacja handlu pozwoleniami na emisje z wykorzystaniem
modelu dla systemu wieloagentowego
177
Tabela 2. Wyniki otrzymane przy załoeniu rynku idealnego
Kraj
USA
EU
Japonia
CANZ
WNP
Emisja
kocowa
MtC/rok
1562
959
321
248
808
Cena
równowagi
USD/tC
143
143
143
143
143
Liczba zak.
Koszt pozwole
pozwole Mt/rok MUSD/rok
Koszt red. emisji
MUSD/rok
310
100
63
33
-506
18523,7
5515,1
2074,3
4638,2
6439,5
11974,3
15790,6
29987,6
16077,6
-73830,3
ródło: Opracowanie własne.
Wobec tego wyniki przedstawione w tabelach obrazujcych najwiksz i najmniejsz
uzyskan warto funkcji celu oblicze (dla 10 przeprowadzonych symulacji), czyli najwikszy
i najmniejszy zysk krajów biorcych udział w handlu, w stosunku do sytuacji, gdyby tego handlu
nie było. Naley zauway, e w nowych modelach nie ma ju idealnie równej kocowej ceny
równowagi dla całego rynku, tak jak w podejciu tradycyjnym (Tab. 2, kolumna nr 3). Wynika to
z tego, e ceny negocjowane s indywidualnie pomidzy kontrahentami i zale od ich warunków
opłacalnoci przeprowadzenia transakcji oraz „umiejtnoci” negocjacyjnych, wobec czego nie
powstaje idealny punkt równowagi cen całego rynku, a jedynie bilateralne punkty równowagi,
w których transakcje kupna sprzeday pomidzy dowolnymi stronami staj si ju nieopłacalne
i nie moe doj do adnej nowej transakcji. Oczywicie ten nowy punkt równowagi, czy te
zestaw kilku punktów, nie odbiega bardzo od wartoci teoretycznych uzyskanych z pierwszego
modelu. Naley take pamita, e teoretyczna cena kosztów redukcji emisji jest jedynie jednym
z czynników kosztu całej transakcji w nowym modelu rynku i wobec tego wartoci zamieszczone
w kolumnie 3 Tab. 3–6 nie musz by sobie równe w punkcie równowagi rynku. Widoczne jest
(Tab. 3–6), e wyniki otrzymywane z modelu jedno- i wielokryterialnego s do zblione, jedynie
koszty zakupów s nieco wiksze w modelu wielokryterialnym, przez co bardziej zyskuj
sprzedajcy (wybrano do zaprezentowania wyniki o skrajnych wartociach z 10
przeprowadzonych symulacji dla kadego modelu).
Tabela 3. Wyniki otrzymane przy wykorzystaniu modelu jednokryterialnego
(najnisze ceny transakcji)
Kraj
USA
EU
Japonia
CANZ
WNP
Emisja kocowa
MtC/rok
Cena kocowa
USD/tC
Liczba zak.
pozwole Mt/rok
Koszt pozwole
MUSD/rok
Koszt red. emisji
MUSD/rok
1562,0
959,0
321,0
248,0
808,0
142,3
143,2
143,1
143,4
142,2
311
99
63
33
-506
32055,6
10593,3
6760,6
1695,1
-51104,6
18381,1
5657,5
2074,3
4638,2
6439,5
ródło: Opracowanie własne.
178
POLSKIE STOWARZYSZENIE ZARZDZANIA WIEDZ
Seria: Studia i Materiały, nr 33, 2010
Tabela 4. Wyniki otrzymane przy wykorzystaniu modelu jednokryterialnego
(najwysze ceny transakcji)
Kraj
USA
EU
Japonia
CANZ
WNP
Emisja kocowa
MtC/rok
Cena kocowa
USD/tC
Liczba zak.
pozwole Mt/rok
Koszt pozwole
MUSD/rok
Koszt red. emisji
MUSD/rok
1562,0
959,0
321,0
248,0
808,0
142,3
143,2
143,1
143,4
142,2
311
99
63
33
-506
50222,9
15014,8
14420,0
1741,7
-81399,3
18381,1
5657,5
2074,3
4638,2
6439,5
ródło: Opracowanie własne.
Tabela 5. Wyniki otrzymane przy wykorzystaniu modelu wielokryterialnego
(najnisze ceny transakcji)
Kraj
USA
EU
Japonia
CANZ
WNP
Emisja kocowa
MtC/rok
Cena kocowa
USD/tC
Liczba zak.
pozwole Mt/rok
Koszt pozwole
MUSD/rok
Koszt red. emisji
MUSD/rok
1560,0
960,0
321,0
249,0
808,0
143,4
141,4
143,1
141,2
142,2
309
100
63
34
-506
41539,7
17357,0
11777,9
2077,5
-72752,1
18666,8
5515,1
2074,3
4495,9
6439,5
ródło: Opracowanie własne.
Tabela 6. Wyniki otrzymane przy wykorzystaniu modelu wielokryterialnego
(najwysze ceny transakcji)
Kraj
USA
EU
Japonia
CANZ
WNP
Emisja kocowa
MtC/rok
Cena kocowa
USD/tC
Liczba zak.
pozwole Mt/rok
Koszt pozwole
MUSD/rok
Koszt red. emisji
MUSD/rok
1562,0
959,0
321,0
248,0
808,0
142,3
143,2
143,1
143,4
142,2
311
99
63
33
-506
67191,8
17419,6
10834,2
2173,6
-97619,3
18381,1
5657,5
2074,3
4638,2
6439,5
ródło: Opracowanie własne.
6. Podsumowanie
Algorytmy agentowe i ewolucyjne to dobre narzdzia symulacji i analizy zjawisk
ekonomicznych. Pozwalaj one wzi pod uwag znacznie wicej parametrów ni przy uyciu
typowych metod analizy, m.in. odchodzc od nierealistycznego załoenia rynku idealnego
w handlu pozwoleniami na emisj. Zbadanie wpływu cen zakupu zdecydowanie bliszych
rzeczywistym i ewentualne zasymulowanie wpływu negocjacji cen na koszty ich zakupu staje si
do łatwym zadaniem, dziki uyciu specjalizowanego algorytmu ewolucyjnego i rozszerzonego
modelu zjawiska zaproponowanego w tej pracy.
Jarosław Staczak
Symulacja handlu pozwoleniami na emisje z wykorzystaniem
modelu dla systemu wieloagentowego
179
%LEOLRJUDILD
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
Alkemade F., La Poutre H. i Amman H.M.: Robust evolutionary algorithm design for
socio-economic simulation. Computational Economics, 28, 2006, s. 355–470.
Bartoszczuk P.: Tradable emission permits as efficient strategy for achieving
environmental goals. Proceedings of The International Workshop on Uncertainty in
Greenhouse Gas Inventories: Verification, Compliance and Trading, Warszawa 2004,
s. 143–150.
Bartoszczuk P. i Horabik J.: Tradable permit systems: considering uncertainty in emission
estimates. Water Air Soil Pollution: Focus 7, 2007, s. 573–579.
Bartoszczuk P.: Minimizing the cost of abatement under imperfectly observed emissions,
Proceedings of 2nd International Workshop on Uncertainty in Greenhouse Gas
Inventories, IIASA, Laxenburg 2007, Austria, 1–8.
Clemens C. i Riechmann T.: Evolutionary dynamics in public good games.
Computational Economics, 28, 2006, s. 399–420.
Ermoliev Y., Michalevich M. i Nentjes A.: Markets for tradable emission and ambient
permits: a dynamic approach. Environmental and Resource Economics, 15, 2000,
s. 39–56.
Godal O.: Simulating the Carbon Permit Market with Imperfect Observations of
Emissions: Approaching Equilibrium through Sequential Bilateral Trade. Interim Report
IR-00-060, IIASA, Laxenburg 2000, Austria.
Horabik J.: On the costs of reducing GHG emissions and its underlying uncertainties in
the context of carbon trading. Raport Badawczy RB/34/2005, IBS PAN, 2005.
Klaasen G., Nentjes A. i Smith M.: Testing the dynamic theory of emissions trading:
Experimental evidence for global carbon trading. Interim Report IR-01-063, IIASA,
Laxenburg 2001, Austria.
180
POLSKIE STOWARZYSZENIE ZARZDZANIA WIEDZ
Seria: Studia i Materiały, nr 33, 2010
SIMULATION OF EMISSION PERMITS TRADING USING MODEL DESIGNED FOR
MULTI-AGENT SYSTEM
Summary
This article describes the problem of the CO2 emission permits market and
introduces several important changes to the standard model, in particular a new
goal function, transactions with price negotiations between regions and – as
a consequence of introducing permit prices – the possibility of investigating the
influence of purchase/sale prices on the market. An additional novelty is the method
of simulating such a market, which is based on a specialized evolutionary algorithm
(EA).
Keywords: emission permits trading, Kyoto Protocol, evolutionary algorithm
Jarosław Staczak
Instytut Bada Systemowych
Newelska 6, 01-447 Warszawa
e-mail: [email protected]