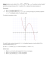Równania Maxwella i równanie falowe

Równania Maxwella i równanie falowe
Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze
opracowanie chronione jest prawem autorskim. Wykorzystanie
niekomercyjne dozwolone pod warunkiem podania źródła.
© Sergiusz Patela 1998-2004
Równania Maxwella
&
&
∂B
∇× E = −
∂t
&
& ∂D &
∇× H =
+J
∂t
&
∇⋅D = ρ
&
∇⋅B = 0
J = gęstość prądu [A/m2],
ρ = gęstość ładunku [C/m3]
Równania
materiałowe:
Z definicji
© Sergiusz Patela, 1998-2004
&
&
& &
D = ε E = ε0 E + P
&
&
& &
B = µ H = µ0 H + M
µ 0 = 4π ⋅10−7 N ⋅ A−2
ε0 ⋅ µ 0 = c −2
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
3
Wielkości fizyczne w równaniach Maxwella
Symbol
Wielkość fizyczna
Jednostka SI
Oznaczenie
E
Natężenie pola elektrycznego
Volt na metr
V/m
D
Indukcja elektryczna
Coulomb na metr kwadratowy
C / m2
P
Polaryzacja
H
Natężenie pola magnetycznego
Amper na metr
A/m
M
Magnetyzacja
j
Gęstość prądu
Amper na metr kwadratowy
A / m2
B
Indukcja magnetyczna
Tesla
ρ
Gęstość ładunku elektrycznego
Coulomb na metr sześcienny
C / m3
σ
Przewodność elektryczna
Siemens na metr
S/m
µ
Przenikalność magnetyczna
Henr na metr
H/m
ε
Przenikalność elektryczna
Farad na metr
F/m
Symbol
Wielkość fizyczna
T
Wartość
c
Szybkość światła w próżni
2.998 x 108 m/s
µ0
Przenikalność magnetyczna próżni
4p x 10-7 H/m
ε0
Przenikalność elektryczna próżni
8.854 x 10-12 F/m
© Sergiusz Patela, 1998-2004
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
4
Operatory różniczkowe
Gradient
Dywergencja
∇ Φ (x , y , z ) =
∂Φ ∂Φ ∂Φ i +
j+
k
∂x
∂y
∂z
&
∂ Fx ∂ F y ∂ Fz
∇ ⋅ F (x , y , z ) =
+
+
∂x
∂y
∂z
Rotacja
i
&
∂Fy 
 ∂F
∂ Fz   ∂ F y ∂ Fx  ∂
 ∂F
∇ × F (x , y , z ) =  z −
−
 j+
 i +  x −
k =
 ∂z
∂z 
∂x 
∂y 
∂x
 ∂y
 ∂x
Fx
Operator Laplace’a
© Sergiusz Patela, 1998-2004
j
∂
∂y
Fy
k
∂
∂z
Fz
∂ 2Φ ∂ 2Φ ∂ 2Φ
∇ Φ =
+
+
∂x 2
∂y 2
∂z 2
2
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
5
Tożsamości operatorowe (wektorowe)
&
&
&
&
2
ro t ro t F = ∇ × ∇ × F = ∇ ∇ ⋅ F − ∇ F
(1)
&
&
&
&
&
&
∇⋅ F ×G = G ⋅ ∇×F − F ⋅ ∇×G
(2)
(
(
)
)
(
(
)
)
(
&
&
&
∇ × Φ F = Φ∇ × F + ∇Φ × F
&
&
&
∇ ⋅ ΦF = Φ∇ ⋅ F + F ⋅ ∇Φ
(
(
)
)
)
(3)
(4)
F, G - wektory, Φ - skalar
© Sergiusz Patela, 1998-2004
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
6
Warunki brzegowe wektorów indukcji
&
∫ ∇ ⋅ FdV =
Twierdzenie Ostrogradskiego - Gaussa
∫
&
&
F ⋅ dS
n
S
2
&
∇⋅B = 0
w. brzeg. dla pola B
1
&
0 = ∫ ∇ ⋅ B dV
V
=
∫
& &
&
&
&
&
B d S = nˆ ⋅ B 2 − nˆ ⋅ B1 = nˆ ⋅ ( B 2 − B1 )
S
&
D
∇⋅ = ρ
w. brzeg. dla pola D
σ =
© Sergiusz Patela, 1998-2004
∫ ρ dV
= nˆ ⋅ ( D 2 − D 1 )
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
7
Warunki brzegowe wektorów natężenia
&
&
∫ ∇ × F ⋅ dS =
twierdzenie Stokesa
R. Maxwella
Całkujemy po poweirzchni
C
2
1
&
&
&
∂ D
∇× H =
+ J
∂ t
&
∫ ∇ × H dS =
S
w. brzeg. dla pola H
∫
& &
F ⋅ dl
&
&
∂ D
∫S  ∂ t + J  dS
tw. Stockesa
0
&
&
&
n × H1 − H 2 = K
(
w. brzeg. dla pola E
)
&
&
∂ B
∇×E = −
∂ t
&
&
n × E1 − E 2 = 0
(
© Sergiusz Patela, 1998-2004
)
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
8
Warunki brzegowe - podsumowanie
Składowe normalne
&
&
nˆ ⋅ ( B 2 − B1 ) = 0
&
&
ˆn ⋅ ( D 2 − D 1 ) = σ
Składowe styczne
&
&
&
n × H1 − H 2 = K
(
)
&
&
n × E1 − E 2 = 0
(
© Sergiusz Patela, 1998-2004
)
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
9
Wyprowadzenie równania falowego (ośrodek jednorodny)
Na pierwsze z równań Maxwella
działamy lewostronnie operatorem
rotacji
&
&
 ∂B 

∇ × ∇ × E = ∇ × −

 ∂t 
Lewą stronę równania przekształcamy
korzystając z tożsamości operatorowej
∇ × ∇ × E = grad divE − ∇ 2 E
(
)
Przy braku ładunków objętościowych div E = 0
&
&
 ∂B 

∂H
 = ∇ × − µ
∇ × −


∂t
 ∂t 

Prawa strona

=


jeżeli założymy, że ośrodek jest jednorodny i izotropowy ( µ = const) to:
za rot H podstawiamy drugie
równanie Maxwella:
&
& ∂D
∇× H =
∂t
wyprowadziliśmy równanie falowe:
© Sergiusz Patela, 1998-2004
&
∂
= −µ
∇× H =
∂t
&
2
(
= − µε
)
∂ E
∂ t2
&
2
&
∂ E
∇ 2 E − µε 2 = 0
∂t
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
14
Równania falowe dla ośrodka jednorodnego
&
2
&
∂ E
2
∇ E − µε
2 = 0
∂t
&
2
&
∂ H
∇ 2 H − µε
2 = 0
∂t
Rozwiązania mogą mieć postać (fala płaska)
&&
i ωt − kr
ψ=e(
gdzie:
© Sergiusz Patela, 1998-2004
)
k = ω με
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
15
Postać równania falowego dla fali płaskiej
Jednym z rozwiązań równania falowego:
&
&
∂ E
2
∇ E − µε
2 = 0
∂t
2
są funkcje postaci (fala płaska):
E = E 0 e j (ω t − β z )
β - stała propagacji (rzut wektora falowego na kierunek propagacji z)
© Sergiusz Patela, 1998-2004
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
26
Układ współrzędnych i struktura światłowodu planarnego
Y
X
0
Z
-t
Rozwiązanie w strukturze planarnej
(mody TE):
Równanie falowe
&
E y = E 0 y ( x ) exp [ j (ω t − β z )]
&
∂ 2E
∇ E − µε
2 = 0
∂t
2
Podstawiając postulowane rozwiązanie do równania falowego
otrzymamy:
∂ 2 E0 y
∂x
2
[
2
− k −β
© Sergiusz Patela, 1998-2004
2
]E
0y
=0
gdzie:
ω
2π
=
k =
v
λ
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
, v=
1
µε
27
Wyprowadzenie równania falowego w strukturze
światłowodu planarnego - mody TE (1)
∂2E y
∂x 2
∂2E y
=
∂y 2
∂2E y
∂t
2
∂y 2
[
∂x 2
∂2E y
+
+
∂2E y
∂z 2
− µε
∂2E y
∂t 2
=0
∂ E 0 y (x )  ∂ 2 E 0 y (x )
∂  ∂
∂ 

ex p i (ω t − β z )
=
E ( x ) ex p i (ω t − β z )  =
=
 ex p i (ω t − β z )

2
∂x
∂
∂x  ∂x 0 y
x
 ∂x 

∂2E y
∂z
∂2E y
2
=
]
[
]
[
]

∂  ∂
E 0 y ( x ) ex p i (ω t − β z )  = 0

∂y  ∂y

[
=
]
∂  ∂
∂

E 0 y ( x ) e x p i (ω t − β z )  =
− i β E 0 y ( x ) e x p i (ω t − β z )

∂z  ∂z
∂z

[
]
{
]} = − β
[
∂  ∂
∂

E 0 y ( x ) ex p i (ω t − β z )  =
i ω E 0 y ( x ) ex p i (ω t − β z )

∂t  ∂t
 ∂t
© Sergiusz Patela, 1998-2004
[
]
{
[
]} = − ω
[
]
[
]
2
E 0 y ( x ) e x p i (ω t − β z )
2
E 0 y ( x ) ex p i (ω t − β z )
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
28
Wyprowadzenie równania falowego w strukturze
światłowodu planarnego - mody TE (2)
∂ 2 E 0 y (x )
2
exp
0
(
)
[
]
i
t
z
E 0 y (x )exp [i (ω t − β z )]−
ω
−
β
+
−
β
∂x 2
− µε {− ω 2 E 0 y (x )exp [i (ω t − β z )]}= 0
∂ 2 E (x )
− [β 2 − µ εω 2 ]E ( x ) = 0
2
∂ x
n=
∂ 2E0 y
∂ x2
c
,
v
1
,
µ 0ε 0
c=
+ [k − β
2
2
]E
0y
v =
= 0
1
µε
lu b :
np. B. Crosignani, ... Światłowody tlekeomunikacyjne,
J. E. Midwinter, Światłowody telekomunikacyjne
© Sergiusz Patela, 1998-2004
k =
ω
ω
2π
2π
=
n=
n=
λ
λ0
c
v
∂ 2 E (x )
−
2
∂ x
 2 ω2 2
β − c 2 n  E (x ) = 0


np. T. Temir, Integrated Optics,
A. Yariv, Optical waves in crystlas
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
29
Warunki brzegowe dla światłowodu planarnego - mody TE
&
&
n × E1 − E 2 = 0
(
&
&
&
n × H1 − H 2 = K
)
(
)
Mod TE posiada tylko jedną niezerową składową pola elektrycznego - Ey,
i dwie składowe pola magnetycznego - Hz i Hy
E y ( x , z , t ) = E 0 y ( x )e i ( ω t − β z )
&
&
∂ B
∇×E =−
∂t
Z pierwszego r. Maxwella
+ def. operatora rotacji
Z harmonicznej zależności od czasu
H 0z = −
Warunki brzegowe:
© Sergiusz Patela, 1998-2004
∂E0 y
∂x
−
∂E y
∂x
−
∂E x
∂Bz
= −
∂y
∂t
∂E0 x
= − iω µ H 0 z
∂y
1 ∂E0 y
i ∂E0 y
=
iω µ ∂ x
ω µ ∂x
E0y1=E0y2
∂ E 0 y1 ∂ x = ∂ E 0 y 2 ∂ x
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
30
Pytania kontrolne
1. Równania Maxwella - wymienić i opisać
2. Wyprowadzić równanie falowe
3. Warunki brzegowe – wymienić i wyjaśnić pojęcie
4. Jak zmieni się postać warunków brzegowych jeżeli
ustalimy układ współrzędnych i postać struktury. Wyjaśnić
na przykładzie światłowodu planarnego.
© Sergiusz Patela, 1998-2004
Podstawy teorii światłowodów. Równania Maxwella i równanie falowe
31