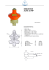analiza częstotliwościowa układu ze sprężyną magnetyczną przy

analiza częstotliwościowa układu ze sprężyną magnetyczną przy

MODELOWANIE INŻYNIERSKIE
41, s. 363-370, Gliwice 2011
ISSN 1896-771X
ANALIZA CZĘSTOTLIWOŚCIOWA
UKŁADU ZE SPRĘŻYNĄ MAGNETYCZNĄ
PRZY WYMUSZENIU KINEMATYCZNYM
JACEK SNAMINA, PIOTR HABEL
Katedra Automatyzacji Procesów, Akademia Górniczo-Hutnicza w Krakowie
e-mail: [email protected], [email protected]
Streszczenie. Praca zawiera analizę częstotliwościową drgań obiektu z układem
wibroizolacji, w którym wykorzystano sterowaną sprężynę magnetyczną.
Sprężyna magnetyczna składa się z magnesów neodymowych oraz cewek
kształtujących pole magnetyczne. Zmiana natężeń prądów płynących w cewkach
daje możliwość sterowania polem magnetycznym, co umożliwia wytworzenie
odpowiedniej siły oddziaływania sprężyny magnetycznej na obiekt chroniony.
1. WSTĘP
Zagadnienia aktywnej wibroizolacji są przedmiotem prac koncepcyjnych i aplikacyjnych
w wielu ośrodkach badawczych. Do układów wibroizolacji wprowadzane są nowe elementy
oraz elementy dotychczas stosowane, lecz o udoskonalonej konstrukcji. Należą do nich
sprężyny magnetyczne, będące elementami tak układów pasywnych, jak i układów
aktywnych. Pasywny układ wibroizolacji płyty wykorzystujący sprężynę magnetyczną został
przedstawiony w pracy [1]. Układ wykorzystujący siłę odpychania magnesów wraz z
równolegle zamontowaną sprężyną został opisany w [2]. Autorzy opracowali model
teoretyczny oraz numeryczny, a następnie potwierdzali jego prawidłowość badaniami
eksperymentalnymi. Patent [3] przedstawia możliwość zmiany siły oddziaływania pomiędzy
magnesami w wyniku obrotu magnesu sześciennego. Wadą tego urządzenia są duże rozmiary
oraz liczne elementy. Zaproponowana w niniejszej pracy prototypowa konstrukcja sprężyny
magnetycznej posiada znacznie mniej skomplikowaną budowę oraz mniejszą liczbę
elementów.
Układ wibroizolacji wykorzystujący sprężynę magnetyczną ma cechy układu
nieliniowego, będące konsekwencją nieliniowej charakterystyki sprężyny. Projektowanie
takich układów w sposób szczególny wymaga indywidualnego podejścia oraz właściwego
doboru parametrów konstrukcyjnych. Aktywny układ wibroizolacji zastosowany do redukcji
drgań obiektu o jednym stopniu swobody wykorzystujący sprężynę magnetyczną z
wymuszeniem dynamicznym przedstawiono w [4]. Charakterystyki częstotliwościowe
układów nieliniowych zostały omówione w pracach [5, 6, 7]. Przedstawiono w nich również
najczęściej stosowane metody analizy częstotliwościowej wykorzystujące metodę bilansu
harmonicznych, metodę Galerkina, metodę iteracyjną oraz metodę małego parametru.
364
J. SNAMINA, P.HABEL
2. BUDOWA I CHARAKTERYSTYKI SPRĘŻYNY MAGNETYCZNEJ
Sprężyna magnetyczna została skonstruowana jako urządzenie, które będzie wykorzystane
przede wszystkim w aktywnych układach wibroizolacji. Zmieniając natężenie prądu
płynącego w cewkach, można sterować siłą wytwarzaną przez sprężynę. Cewki będące
elementem układu magnetycznego sprężyny są zasilane z zewnętrznego, sterowanego źródła
prądu.
2.1. Zasada działania
Schemat sprężyny magnetycznej przedstawiono na rys. 1. Dwa neodymowe magnesy
górne (1) zamocowane są do końca trzpienia prowadzącego (7), a kolejne dwa (2) do
obudowy w punkcie leżącym w osi sprężyny. Magnesy zostały zamocowane w taki sposób,
aby siły oddziaływania pomiędzy nimi były siłami odpychającymi. Trzpień prowadzący (7)
umożliwia ruch magnesów górnych (1) w osi sprężyny – dzięki umieszczeniu go w łożysku
liniowym (8). Obwód magnetyczny składa się z czterech rozgałęzień bocznych (3), na
których znajdują się cewki (6), części górnej (4) oraz części dolnej (5), do której
przymocowane są magnesy dolne (2). Odpowiednie ułożenie wszystkich elementów zapewnia
obudowa górna (9) oraz dolna (10) – połączone ze sobą za pomocą czterech prętów
stabilizujących konstrukcję (11). Umieszczone w obwodzie magnetycznym cztery cewki (6)
wpływają na rozkład pola magnetycznego w przestrzeni pomiędzy magnesami. Dzięki
zmianie natężenia prądów płynących w cewkach istnieje możliwość sterowania polem
magnetycznym, a w efekcie siłą sprężyny.
7
8
9
4
11
6
1
5
3
10
2
Rys. 1. Schemat sprężyny magnetycznej
2.2. Badania laboratoryjne
Zdjęcie stanowiska laboratoryjnego przedstawiono na rys. 2. Układ napędowy wzbudnika
drgań wyposażono w siłownik hydrauliczny (H) dwustronnego działania z jednostronnym
tłoczyskiem posiadającym wbudowany czujnik położenia BALLUFF BTL5. Siłownik
hydrauliczny (H) jest sterowany za pomocą serwozaworu (S) MOOG model D761-104 typ
S63FOFMAVPL oraz zasilany przez agregat hydrauliczny (A). Zadane wymuszenie
kinematyczne platformy dolnej (PD) – do której jest przymocowana obudowa sprężyny
magnetycznej (O) – jest realizowane za pomocą siłownika hydraulicznego (H). Czujnik siły
ANALIZA CZĘSTOTLIWOŚCIOWA UKŁADU ZE SPRĘŻYNĄ MAGNETYCZNĄ …
365
(F) ZEPWN Typ CL 16 Nr 4374 jest zainstalowany w osi sprężyny pomiędzy trzpieniem
prowadzącym (W) a platformą górną (PG). Siła oddziaływania sprężyny magnetycznej w
badanym układzie to siła działająca między obudową sprężyny (O) a trzpieniem
prowadzącym sprężyny (W) oraz jednocześnie między platformą dolną (PD) a platformą
górną (PG). Platforma górna (PG) została utwierdzona. Wraz ze zmianą położenia platformy
dolnej (PD) następuje zmiana siły oddziaływania pomiędzy magnesami. Cewki (C)
zainstalowane na specjalnie skonstruowanym magnetowodzie są zasilane z zasilaczy
stałoprądowych (Z) MeanWell SP-320-24. Wyniki przeprowadzonych badań laboratoryjnych
są zgodne z wynikami obliczeń wykonanych metodą elementów skończonych potwierdzają
obliczenia symulacyjne wykonane MES przy użyciu programu ANSYS. Błąd względny
wyników obliczeń siły oddziaływania sprężyny nie przekracza 13%, co jest wynikiem
zadowalającym przy przyjętych uproszczeniach.
PG
Z
F
W
C
A
H
O
S
PD
Rys. 2. Stanowisko laboratoryjne
3. RÓWNANIE RUCHU BADANEGO UKŁADU
Rozważany układ przedstawiono schematycznie na rys. 3. Układ ten jest układem o
jednym stopniu swobody, w którym ruch ciała o masie m jest wymuszany ruchem podłoża.
Do wibroizolacji ciała wykorzystano sprężynę magnetyczną, której budowa i własności
zostały przedstawione w poprzednim rozdziale. Na rys. 3. zaznaczono również blok
oznaczający jednostkę sterującą, która na podstawie sygnałów związanych z ruchem układu
wyznacza sygnał sterujący sprężyną magnetyczną. Współrzędna x opisuje położenie ciała o
masie m względem położenia równowagi statycznej. Równanie drgań wymuszonych
rozważanego układu ma postać:
mx&& = Fmag + Fmag ( stat ) − mg
(1)
(stat)
oznacza składową siły sprężyny magnetycznej przy braku zasilania cewek
Gdzie Fmag
(składowa stała sprężyny). Fmag oznacza składową zmienną siły w sprężynie związaną z
przepływem prądu przez cewki. Siła Fmag(stat) równoważy siłę ciężkości mg. Ze względu na
równowagę siły ciężkości oraz składowej stałej siły w sprężynie, masa ciała oraz magnesy
stałe muszą być odpowiednio dobrane. Zbudowany prototyp sprężyny został zaprojektowany
dla masy m=30 [kg].
366
J. SNAMINA, P.HABEL
x , x&
x
jednostka
sterująca
m
sprężyna
magnetyczna
sygnał
sterujący
DC
+-
y , y&
y
Rys. 3. Schemat układu
4. ALGORYTM STEROWANIA
Sterowanie siłą oddziaływania sprężyny magnetycznej jest realizowane przez odpowiednie
zasilanie cewek. Przyjęto prosty w realizacji algorytm sterowania, w którym natężenie prądu
jest proporcjonalne do prędkości ciała względem ruchomego podłoża. Taki algorytm
sterowania prądem prowadzi do nieliniowej zależności siły Fmag od prędkości względnej w
związku z nieliniową charakterystyką sprężyny, która opisuje siłę w funkcji względnego
położenia magnesów oraz prądu zasilającego cewki. Symbolem ξ oznaczono
przemieszczenie względne magnesów, a symbolem i natężenie prądu zasilającego cewki. Na
rys. 4 przedstawiono wykres siły Fmag (ξ , i ) otrzymany na podstawie pomiarów
laboratoryjnych. Wykorzystano charakterystyki statyczne sprężyny dla natężenia prądu
i = {−7,0,7} [A] – przepływającego przez wszystkie cewki. Ujemna wartość natężenia prądu
oznacza taki kierunek przepływu prądu przez cewki, przy którym następuje osłabienie pola
magnetycznego między magnesami. Dla prędkości ξ& =0 [m/s] cewki są nieaktywne, gdyż
zgodnie z przyjętym algorytmem i=0, wtedy wartość siły Fmag została aproksymowana
wielomianem Fmag (ξ ,0) = a3 ⋅ ξ 3 + a1 ⋅ ξ + a0 . W przypadku zasilania cewek prądem o
natężeniu
i=7
[A]
wielomian
aproksymujący
ma
inne
współczynniki
Fmag (ξ ,7) = b3 ⋅ ξ 3 + b1 ⋅ ξ + b0 . Dla prądu o natężeniu i=-7 [A] wielomian aproksymujący ma
postać Fmag (ξ , −7) = c3 ⋅ ξ 3 + c1 ⋅ ξ + c0 . Jednostka sterująca przelicza natężenie prądu i w
zależności od aktualnej wartości prędkości względnej ξ& . Prąd o natężeniu i =7 [A] jest
sygnałem sterującym w przypadku ξ& = ξ& max, natomiast prąd o natężeniu i=-7 [A] jest
sygnałem sterującym w przypadku ξ& = −ξ&max .
ANALIZA CZĘSTOTLIWOŚCIOWA UKŁADU ZE SPRĘŻYNĄ MAGNETYCZNĄ …
367
400
300
400
200
]
N
[
g
a
m
Fmag (ξ , i = 7)
200
100
0
0
F
Fmag (ξ , i = 0)
-200
7
5
-100
Fmag (ξ , i = −7)
3
1 0
-1
i [A]
-3
-5
-7
-8
-6
-4
-2
0
2
4
8
6
-3
ξ [m]
-200
-300
x 10
Rys. 4. Składowa zmienna siły wytwarzanej przez sprężynę magnetyczną w funkcji
współrzędnej ξ oraz natężenia prądu i
5. ANALIZA CZĘSTOTLIWOŚCIOWA
Analizę częstotliwościową układu wykonano metodą bilansu harmonicznych. Obliczenia
symulacyjne przeprowadzono z zastosowaniem programu MATLAB R2009b.
Na podstawie równania (1), po uwzględnieniu równowagi siły ciężkości i składowej stałej
w sprężynie, równanie drgań ciała o masie m przyjmuje postać:
mx&& = Fmag (ξ , i )
(2)
Wprowadzając przemieszczenie względne ξ = y − x równanie ruchu może zostać zapisane
w formie:
(3)
mξ&& + F% (ξ , ξ&) = my&&
Gdzie F% (ξ , ξ&) oznacza składową zmienną siły w sprężynie, po uwzględnieniu
proporcjonalności natężenia prądu i do prędkości względnej ξ& , według założonego algorytmu
sterowania.
Zgodnie z założeniem metody bilansu harmonicznych przyjmujemy: sinusoidalnie
zmienne wymuszenie y = y0 sin(ωt + ϕ ) , podstawową harmoniczną przemieszczenia
bezwzględnego w postaci x = x0 sin(ωt +ψ ) oraz podstawową harmoniczną przemieszczenia
względnego ξ = ξ0 sin(ωt ) . We wzorach uwzględniono przesunięcie fazowe ϕ oraz ψ .
W wyniku zastosowania algorytmu obliczeń metodą bilansu harmonicznych uzyskano
następujące równanie krzywej rezonansowej:
2
⎛
ω 2 d3ξ0 4 ω 2 d1ξ0 2 ⎞ 2 ω 2e02ξ0 2
3
2
2
ξ + & 2 = m 2 y0 2ω 4
+
⎜ − mω + a3ξ 0 + a1 +
& 2
& 2 ⎟ 0
ξ
ξ
4
16
8
4ξ max
max
max
⎝
⎠
(4)
368
J. SNAMINA, P.HABEL
Współczynniki dk i ek zostały
wprowadzone jako pomocnicze według
następującej zależności: dk=bk+ck-2ak
oraz ek=bk-ck dla k=0,1,3. Maksymalną
prędkość
wyznaczono
na
ξ&max
podstawie obliczeń symulacyjnych.
Przykładowy
wynik
obliczeń
przedstawiono w postaci trajektorii
fazowej na rys. 5. Maksymalna
prędkość podczas ruchu ustalonego ma
wartość ξ&max =0.16 [m/s].
Krzywa szkieletowa przedstawia
zależność częstości rezonansowej od
amplitudy, przy braku wymuszenia. Ma
ona następującą postać:
i ∈ <-7;7> [A]
i = 0 [A]
0.4
0.2
]
s/
m
[
t
d/
ξ
d
0
-0.2
-0.4
-0.015
-0.01
-0.005
0
0.005
0.01
ξ [m]
Rys. 5. Trajektoria fazowa ruchu: y0=0.002 [m],
ω=30 [rad/s]
a1 3 a3 2
(5)
+
ξ0
m 4m
Dla amplitudy ξ0=0 częstość drgań własnych wynosi ω0=30,08 [rad/s] i wzrasta wraz ze
wzrostem amplitudy ξ0. Wykres zależności (5) przedstawiono na rys.6.
ω=
0.015
]
m
[
ξ
0
0.01
0.005
0
0
5
10
15
20
25
30
35
40
45
50
ω [rad/s]
Rys. 6. Krzywa szkieletowa
Zależność amplitudy drgań od częstości wymuszenia można przedstawić graficznie w
postaci krzywych rezonansowych – rys. 7 oraz 8. Krzywe rezonansowe wykreślono dla
dwóch wartości amplitudy wymuszenia kinematycznego y0=0.002 oraz y0=0.004 [m].
Rozważany nieliniowy układ porównano do analogicznego liniowego układu o parametrach:
m=30 [kg], c=450 [N⋅s/m] oraz k=27050 [N/m]. Analiza częstotliwościowa przemieszczenia
względnego ξ w zakresie częstości ω∈<1:1000> [rad/s] została przedstawiona na rys. 7a.
Zastosowanie proponowanego układu wykorzystującego sprężynę magnetyczną dla
przyjętego wymuszenia powoduje zwiększenie amplitudy ξ0 w zakresie częstości
okołorezonansowych względem liniowego układu. Wzrost wartości amplitudy y0 powoduje
przesunięcie częstotliwości rezonansowych w kierunku większych częstości. Zależność kąta
Θ = −ϕ , opisującego przesunięcie fazowe sygnału ξ(t) względem y(t), przedstawiono w
postaci charakterystyki fazowo-częstotliwościowej na rys. 7b. Zastosowanie układu
nieliniowego ze sprężyną magnetyczną wpływa na zmianę przesunięcia fazowego Θ w
obszarze częstości okołorezonansowych. Wzrost amplitudy y0 powoduje zwiększenie
przesunięcia fazowego Θ .
ANALIZA CZĘSTOTLIWOŚCIOWA UKŁADU ZE SPRĘŻYNĄ MAGNETYCZNĄ …
369
3
(a)
]
-[
2
y0
/
ξ
0
1
0
0
10
10
1
2
10
3
10
ω [rad/s]
150
(b)
100
]
°[
Θ
50
0
0
10
10
1
2
10
3
10
ω [rad/s]
(
Rys.7. Charakterystyka amplitudowo-częstotliwościowa
oraz fazowo-częstotliwościowa przemieszczenia względnego ξ0
model liniowy,
model nieliniowy y0=0.002 [m],
model nieliniowy y0=0.004[m])
Analiza częstotliwościowa przemieszczenia bezwzględnego x w zakresie częstości
ω∈<1:1000> [rad/s] została przedstawiona na rys. 8a. Zwiększanie wartości amplitudy y0
powoduje przesunięcie częstości rezonansowych w kierunku większych wartości.
Charakterystyka fazowo-częstotliwościowa pokazana na rs. 8b. przedstawia zależność kąta
Γ=ψ−ϕ opisującego przesunięcie fazowe sygnału x(t) względem y(t) od częstości ω.
Zastosowanie układu ze sprężyną magnetyczną powoduje zmianę przesunięcia fazowego Γ
względem układu liniowego. Zwiększanie amplitudy y0 wpływa na zmianę Γ tylko w
obszarze częstości okołorezonansowych.
3
(a)
]
-[
2
y0
/
0
x
1
0
0
10
10
1
2
10
3
10
ω [rad/s]
0
(b)
]
°[
Γ
-50
-100
0
10
1
2
10
10
3
10
ω [rad/s]
(
Rys.8 Charakterystyka amplitudowo-częstotliwościowa
oraz fazowo-częstotliwościowa przemieszczenia bezwzględnego x0
model liniowy,
model nieliniowy y0=0.002 [m],
model nieliniowy y0=0.004[m])
370
J. SNAMINA, P.HABEL
6. WNIOSKI
Uzyskane wyniki pozwalają na analizę zachowania się rozważanego układu wibroizolacji
w zakresie częstości do 1000 [rad/s]. Analiza została przeprowadzona dla zakresu sterowania
prądem o natężeniu w zakresie <0, 7> [A], uwzględniając przy tym przepływ prądu w obu
kierunkach.
Zastosowanie układu ze sprężyną magnetyczną stwarza możliwość sterowania sztywnością
i tłumieniem układu. Opcja sterowania układem tylko w wybranym zakresie częstości (np. dla
częstości okołorezonansowych) jest możliwa do zastosowania w rozważanym układzie.
Takiej możliwości nie ma w konwencjonalnym układzie ze sprężyną i tłumikiem
wiskotycznym.
Możliwość zastosowania większej wartości maksymalnej prądu pozwoliłaby na
zwiększenie efektywności wibroizolacji. Ograniczenie to wynika z warunków
konstrukcyjnych cewek, dla których wykonywano badania laboratoryjne.
Proponowana sprężyna magnetyczna może zostać zastosowana w wibroizolacji maszyn
roboczych oraz siedzisk operatorów maszyn.
Pracę wykonano w ramach projektu badawczego nr N N501 228940.
LITERATURA
1. Puppin E., Fratello V.: Vibration isolation with magnet spring. Review of Scientific
Instruments, 2002.
2. Bonisoli E., Vigliani A.: Passive elasto-magnetic suspensions: nonlinear models and
experimental outcomes. Mechanics Research Communications p. 385–394, 2007.
3. Patent USA nr 6084329: Vibration mechanism having a magnetic spring.
4. Snamina J., Habel P.: Analiza częstotliwościowa układu wibroizolacji ze sprężyną
magnetyczną. Kraków: Wydawnictwo PK, 2010.
5. Meirovitch L.: Elements of vibration analysis. McGraw-Hill Publishing Company, 1986.
6. Łuczko J.: Drgania regularne i chaotyczne w nieliniowych układach mechanicznych,
Kraków: Wyd. PK, 2018.
7. Polina S. Landa: Regular and chaotic oscillations. Springer, 2001.
FREQUENCY ANALYSIS OF A SYSTEM WITH MAGNETIC SPRING
BY KINEMATIC EXCITATION
Summary. The paper presents the frequency analysis of a one degree of freedom
system with kinematic excitation. The system consists of a rigid body and a
magnetic spring. The motion is excited by the basis displacement. The main parts
of the magnetic spring are neodymium magnets and coils forming magnetic field.
The force exerted by the spring can be controlled by changing the current in coils.
The system is nonlinear because characteristics of the spring are nonlinear. The
harmonic balance method was used to carried out the frequency analysis of
considering system.