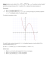Modelowanie przepływu cieczy przez ośrodki porowate Wykład VII

Modelowanie przepływu cieczy przez ośrodki porowate
Wykład VII
ROZWIAZANIA ZAGADNIEŃ PRZEPŁYWU
FILTRACYJNEGO METODAMI ANALITYCZNYMI.
7.1 Przepływ przez groblę z uwzględnieniem zasilania wodami infiltracyjnymi.
Do rozwiązania problemu przyjmiemy aproksymację procesu filtracyjnego Boussinesqa [patrz
rozdział IV monografii] przy założeniu, że upłynął odpowiednio długi czas i możemy proces filtracji
rozpatrywać jako ustalony, więc w równaniu Boussinesqa nie występuje pochodna cząstkowa
wysokości hydraulicznej H po czasie. Rozpatrzymy trzy przypadki:
równania nieliniowego Boussinesqu’a,
równania zlinearyzowanego Boussinesqa przez Boussinesqa,
równania zlinearyzowanego Boussinesqa przez Bagrowa i Wierygina.
Przyjmijmy do rozważań groblę (rys. 22) zasilaną wodami infiltracyjnymi pochodzącymi z
opadów. Jeśli więc grobla będzie zbudowana z ośrodka gruntowego o współczynniku filtracji k = const
i pokryta jednorodną roślinnością, to intensywność infiltracji ε będzie miała również wartość stałą.
Zagadnienie traktujemy jako płaskie, więc zgodnie z założeniami teorii Boussinesqa sprowadza się ono
do zagadnienia jednowymiarowego. Równanie Boussinesqa dla rozważanego przypadku ma postać:
Rys. 22 Schemat przepływu przez groblę z infiltracją.
Hx
dd
H
x
dd
k




+ε = 0.

(7.1)
Zlinearyzowane równanie Boussinesqa przez Boussinesqa ma postać:
r
Hx
dd
Hs
k
2
2
+ε = 0,
(7.2)
natomiast zlinearyzowane równanie Boussinesqa przez Bagrowa – Wierygina można zapisać w
postaci:
x
dd
k
τ
2
+ε = 0,
2
(7.3)
Hs
H
u
r
przy czym τ = 2 2 oraz
określa średnią miąższość strumienia filtrującej wody.
Rozważmy na początku nieliniowe równanie i wprowadźmy nową zmienną :
Hx
dd
H
u
=
.
(7.4)
Wówczas po podstawieniu (7.4) do równania dostajemy:
ux
dd
k
+ε = 0.
(7.5)
Rozwiązaniem powyższego równanie jest funkcja:
C
x
k
u
ε
=−
+
.
(7.6)
Wstawiając do (7.6) podstawienie (7.4) mamy:
=−
ε
C
x
k
Hx
dd
H
(7.7)
+
.
Rozwiązując powyższe równanie różniczkowe metodą rozdzielenia zmiennych dostajemy
funkcję wysokości hydraulicznej w postaci:
C
x
C
x
k
H
ε
= −
+
2
+
1
.
(7.8)
Rozważmy obecnie przypadek zlinearyzowanego równania Boussinesqa w postaci (7.2). Całkując
dwukrotnie po dx równanie (7.2), dostajemy rozwiązanie w postaci:
ε
2
C
x
C
Hs
xk
H
+
+
r
=−
2
1,
(7.9)
Które, jak widać, różni się od rozwiązania (7.8).
Weźmy obecnie pod uwagę zlinearyzowane równanie Boussinesqa przez Bagrowa – Wierygina w
postaci (7.3):
=−
2
ε
k
x
dd
τ
2
.
(7.10)
Całkując dwukrotnie powyższe równanie (7.10) po dx dostajemy:
2
+
C
x
C
2
xk
τ =−
ε
+
1.
(7.11)
H
Wiemy jednak, że τ =
2
2 , więc uzyskujemy rozwiązanie w postaci:
ε
C
x
C
x
k
H
= −
+
2
+
1
,
(7.12)
które jest tożsame z rozwiązaniem nieliniowego równania Boussinesqa (7.8).
= →
oraz dla
H
H
1,
L
=
x
=0→
H
dla
H
C
C x
Rozważając charakter krzywych uzyskanych w rozwiązaniach widać, że w przypadku
nieliniowego równania Boussinesqa i zlinearyzowanego równania Boussinesqa metodą Bagrowa Wierygina otrzymana krzywa jest wycinkiem elipsy, natomiast w przypadku rozwiązania
zlinearyzowanego równania Boussinesqa przez Boussinesqa krzywa reprezentująca zwierciadło
swobodne jest parabolą. W dalszych rozważaniach ograniczymy się tylko do rozwiązań nieliniowego
równania Boussinesqua (7.8), nie wnikając w problem, które z uzyskanych rozwiązań jest bliższe
doświadczeniom.
Stałe
i 1 wyznaczymy dla rozważanego zadania z warunków brzegowych:
=
2.
Po podstawieniu tych wartości do rozwiązania
(7.12) dostaniemy ostateczną postać funkcji wysokości hydraulicznej w postaci:
ε
+
−

2
2
1
−
2
2
H
x
H
L
H
Lk
x
k
H
= −
ε



+
2
1
.
(7.13)
q
Znając funkcję wysokości hydraulicznej możemy wyznaczyć przebieg funkcji prędkości
przypadający na 1mb grobli przepływający przez dowolny przekrój
filtracji oraz wydatek
prostopadły do kierunku filtracji:
2
ε
+

ε
2
1
+
2
−
2
ε
2
1
−
2
1
−
−
2
2
−
2
2
2
2






−
,
2
1
(7.14)
HL
−
ε
H
k
L
=ε
x
v
H
q
=
H
x
H
L
H
L
H
L H
k
L
k
2 −
+
x
k
=−
x
k
k
Hx
dd
k
v
=−
 2ε
−

.
L
x
x
Z praktycznego punktu widzenia najbardziej interesuje nas wydatek po obu stronach grobli
czyli dla = 0 i dla = :
2
)+ε
2
,
L
2
2
L
2
−
H
L
x
(
2
1
)−ε
2
H
k
q
=
=
2
2
L
−
L
x
=
2
1
H
H
k
q
=0
(
(7.15)
.
Stąd różnica:
=0
L
x
L
x
−
q
q
=
=ε ,
(7.16)
co było do przewidzenia, a wynik jest zgodny z przyjętymi warunkami brzegowymi zadania.
s
m
k
Rozważmy przepływ przez groblę wywołany działaniem infiltracji o intensywności ε
−5
= 2*10−7
s
m
Przykład liczbowy.
/ ,
2
u
u
= 100*  −10−2
m
H
HH
ma postać:
H
H
= 10
/ . Początkowy poziom wody wynosi 10m. Odległość L wynosi
gdy współczynnik filtracji
100m. Porównamy rozwiązania uzyskane przy linearyzacji Bousssinesqa i Bagrowa Wierygina.
Zakładając dla obydwu przypadków, że 1 = 2 = 0 = 10
rozwiązanie w pierwszym przypadku
+ 10−2 + 0, 01 ,
0
2
u
= 10 −2*10−2
u
HH
a w drugim przypadku:
+ 2*10−2 + 0, 01 .
0
Wyniki względnej zmiany wysokości hydraulicznej pod wpływem infiltracji przedstawiono na rys. 23
=
xL
i
u
=
HH
f
Rys. 23 Wyniki obliczeń zmiany wysokości hydraulicznej (
)
0
(z wykorzystaniem oprogramowania Mapple 8).
7.2 Dopływ do rowu przy zasilaniu wodami infiltracyjnymi.
W warstwie wodonośnej zbudowanej z gruntu jednorodnego i izotropowego o współczynniku
filtracji k wykonano rów sięgający jej spągu. Jej przekrój prostopadły do osi rowu przedstawiono na rys.
24.
Przed wykonaniem rowu zwierciadło wody było poziome i znajdowało się na wysokości
H
Rys. 24. Schemat zadania dopływu wody do rowu przy zasilaniu wodami infiltracyjnymi.
1
w
H
przyjętym układzie odniesienia. Natomiast po wykonaniu rowu poziom wody ustalił się na wysokości
0 . Warstwa wodonośna zasilana jest w sposób ciągły w czasie wodami opadowymi z intensywnością
C
C
infiltracji ε =const. Równanie Boussinesqa ma postać Błąd! Nie można odnaleźć źródła odwołania..
Rozwiązaniem tego równania, jak pokazano w poprzednim podrozdziale, jest funkcja wysokości
hydraulicznej wyrażona wzorem (7.8). Stałe
i
1 wyznaczymy z następujących warunków
=
oraz dla
Hx
dd
0
R
=
x
=0→
H
Dla
H
x
brzegowych:
→
= 0 gdzie R oznacza zasięg obszaru infiltracji.
Podstawiając powyższe warunki brzegowe do wzoru (7.8), dostaniemy funkcję wysokości hydraulicznej
wyrażoną wzorem:
2
+2
ε
H
x
R
k
ε
x
k
H
= −
+
2
0
.
(7.17)
H
Możemy zadać pytanie; w jakiej odległości R od początku układu współrzędnych wysokość
hydrauliczna osiągnie wartość 1 ? Podstawiając odpowiednie wartości do równania (7.17)
dostaniemy:
=
2
1
H
H
k
R
(
−
2
0
ε
).
(7.18)
Przyjmując układ współrzędnych (jak na rys. 7.13) obliczymy funkcję prędkości filtrującej
wody oraz wydatek na jednostkę długości rowu w postaci:
(
2
1
−
2
0
2
2
)
)
,
H
x
+ 4
−
H
2
ε
2
1
H
k
−
ε
x
k
=−
(
H
H
k
k
x
Hx
dd
k
v
=−
ε
−ε +
+
2
0
(7.19)
+
ε
(
2
1
−
H
= −ε
H
k
k
x
v
H
q
=
2
0
).
Dopływ do rowu na jednostkę jego długości wynosi:
2
1
−
R
(
H
x
= ε
H
k
q
=0
2
0
,
) =ε
(7.20)
co zgodne jest z przyjętymi założeniami zadania.
7.3. Studnia zasilana wodami infiltracyjnymi.
r
W jednorodnej i izotropowej warstwie wodonośnej o współczynniku filtracji k wykonano pionową studnię
o promieniu 0 sięgająca jej spągu (studnia zupełna). Przekrój warstwy wodonośnej przechodzący
przez os studni przedstawiono na rys. 7.15.
Rys. 25. Schemat zadania dopływu wód do studni zasilanej wodami infiltracyjnymi.
Założymy, że są spełnione następujące założenia wstępne:
przepływ jest ustalony, a poziom w studni znajduje się na wysokości
0
ε=
1
ponad
t
s
n
o
c
H
warstwą nieprzepuszczalną,
warstwa wodonośna zasilana jest wodami opadowymi z intensywnością infiltracji
H
spąg warstwy wodonośnej ułożony jest poziomo,
przed pompowaniem zwierciadło wody jest poziome i znajduje się na wysokości
,
ponad warstwą
nieprzepuszczalną.



Hr
dd
H
kr
Hr
dd
H
r
dd
k
Dla powyższego przypadku nieliniowe równanie Boussinesqa ma postać:

+

+ε = 0.
(7.21)
u
:
u
=
Hr
dd
H
Wprowadźmy nową zmienną
.
(7.22)
+
ε
k
+
ur
ur
dd
Podstawiając (7.22) do równania (7.21) dostajemy:
= 0.
Rozwiązaniem powyższego równania (7.23) jest funkcja:
(7.23)
Cr
r
k
u
=−
ε
+
2
.
(7.24)
Uwzględniając (7.22) w (7.24), otrzymujemy równanie różniczkowe:
Cr
r
k
Hr
dd
H
=−
ε
+
2
.
(7.25)
Stąd po rozwiązaniu metodą rozdzielenia zmiennych dostajemy funkcje wysokości
hydraulicznej w postaci:
2
2
+
C
r
ε
C
r
k
H
= −
ln +
.
1
(7.26)
0
=
oraz dla
→
C
=
C
→
i
1
, korzystając z
Hr
dd
0
R
r
=
H
dla
H
r
r
Uzyskane rozwiązanie jest ogólnym rozwiązaniem równania (7.21).
Dla rozpatrywanego przez nas zagadnienia brzegowego obliczymy stałe
warunków brzegowych:
= 0.
Z układu równań otrzymuje wartości stałych:
ε
R
k
C
=
2
ε
2
0
2
−
ε
2
r
+
R
k
H
2
0
=
r
k
C
1
(7.27)
ln
0
Można wiec określić funkcję wysokości hydraulicznej wzorem:
−
2
0
)+ ε
H
rr
2
R
k
2
(
r
ε
r
k
H
= −
2
+
ln
2
0
.
(7.28)
0
Przykład liczbowy.
s
m
przebieg funkcji wysokości hydraulicznej w warstwie gruntu o współczynniku filtracji
zasięg obszaru R=1000m, a poziom wody w studni na wysokości
ε = 2*10−8
0
= 10
m
, zasilanego wodami infiltracyjnymi o intensywności
H
= 10
−5
s
m
k
Obliczmy
.
. Przyjmuje się
r
Rys. 26. Przebieg funkcji wysokości hydraulicznej H w zależności od u=r/R.
Znając funkcję wysokości hydraulicznej możemy obliczyć funkcje prędkości filtracji i
wydatek przepływający przez pobocznicę walca o promieniu i wysokości hydraulicznej H:
)+
ε
2
H
rr
−
2
0
,
+
ln
2
0
0
2
−
r
= πε (
(
R
v
H
r
Q
= 2π
2
2
r
2 −
ε
r
k
=
R
Rr k
r
Hr
dd
k
v
=−
2
−ε + ε
2
(7.29)
).
=
rR
u
Przyjmując te same dane jak w poprzednich obliczeniach wysokości hydraulicznej H
otrzymamy zmienność funkcji prędkości filtracji v w zależności od bezwymiarowej zmiennej
. Poniżej przedstawiono wykres zmiany prędkości z odległości od studni.
Rys. 27. Funkcja prędkości filtracji przy zasilaniu wodami infiltracyjnymi u = r R .
r
r
Dla
=
0
wydatek studni wynosi:
2
r
= πε (
r
r
0
R
Q
=
−
2
0
).
(7.30)
Najczęściej przyjmuje się, że
R
Q
= πε
r
r
=
0
2
,
(7.31)
r
2
0
)+ ε
2
+
ln
H
−
H
2
Rr
2
(
R
k
ε
r
= −
R
k
H
1
H
R
r
a
l
d
gdyż studnia zasilana jest również wodami opadowymi z powierzchni π 02 .
W równaniach od (7.27) do (7.31) występuje nieznana wielkość promienia zasięgu leja depresji
R. Wyznaczyć ją można, kładąc dodatkowy warunek brzegowy:
= → = 1 . Stąd
mamy:
2
0
.
(7.32)
0
Powyższe równanie jest równaniem uwikłanym. Najłatwiej znaleźć wartość R przekształcając
równanie (7.32) do postaci:
)−1 =
2
2
2
0
 
 ln 
 
Rr
ε
2
0
2
0
Rr
−
r
2
1
H
H
k
(
0
 1
 −  .
 2
(7.33)
r
Obliczając lewą stronę równania z wykresu 26 otrzymamy bezpośrednio wartość R. Należy
wziąć pod uwagę, że wielkości rzędnej F na wykresach wykonanych dla różnych wartości 0
wynoszą:
2
1
−
ε
2
0
2
0
r
(
H
H
k
F

= 10 

−6
) − 1  .
(7.34)
2

Rr
Rys. 28. Zależność funkcji F od
0
= 0, 25
, e)
0
= 0,3
m
, d)
r
= 0, 2
m
0
r
, c)
m
= 0,15
r
0
m
= 0,1 , b)
r
0
m
r
a)
dla wartości
0
;
(obliczenia i wykres Mathematica 5).
Jeżeli znamy dopływ wody do studni i intensywność infiltracji ε obliczenia promienia zasięgu zasilania
obliczamy bezpośrednio ze wzoru (7.31).
7.4. Obliczanie pól drenowych.
W typowej kanalizacji polegającej na odprowadzaniu wód ściekowych do gruntu wody ściekowe
przechodzą najpierw przez komory wstępnego oczyszczania, w których oddzielone zostają tłuszcze,
grubsze zawiesiny, a ścieki ulegają fermentacji i później przepływają na pola drenowe, gdzie następuje
ich infiltracja w grunt. Infiltracja w grunt następuje poprzez instalację, która jest identyczna jak typowa
instalacja drenażu poziomego. Przykładowe pole drenowe przedstawiono na rys. 29
Rys. 29. Przykładowe pole drenowe.
W niniejszy podrozdziale zajmiemy się wyznaczeniem maksymalnego zwierciadła wody w obszarze
wpływu pola drenowego, znając wydatek tego pola Q [zakładana objętość wód ściekowych
odprowadzana do gruntu w czasie] i jego powierzchnię F. Maksymalny poziom zwierciadła wody
wyznaczymy przy następujących założeniach wstępnych:
H
pole drenowe jest założone w jednorodnej i izotropowej warstwie wodonośnej o współczynniku
filtracji k,
spąg warstwy wodonośnej położony jest poziomo,
przed założeniem pola drenowego, zwierciadło wody było poziome znajdowało się na
wysokości 0 ponad warstwą nieprzepuszczalną,
warstwa wodonośna zasilana jest wodami opadowymi, przy czym średnia wartość infiltracji przy
maksymalnych opadach rocznych wynosi ε ,
wody ściekowe są równomiernie rozprowadzane na całej powierzchni F.
Aby przy takich warunkach obliczyć pole drenowe, skonstruujmy schemat obliczeniowy - rys. 30.
Rys. 30. Schemat obliczeniowy pola drenowego.
ε1
Wartość infiltracji pod polem drenowym
ε
i załóżmy radialny rozpływ wody.
wyznaczymy ze wzoru:
,
(7.35)
oznacza średnią wartość infiltracji przy maksymalnych opadach rocznych, a
ε
d
gdzie
π
=
d
ε1 = ε + ε
1
F
r
Wprowadźmy zastępczy promień pola drenowego
określa
R
Q
infiltrację wywołaną odprowadzeniem wód ściekowych. Promień oddziaływania pola drenowego R
wyznaczamy ze wzoru:
=
,
π∆ε
(7.36)
przy czym Q oznacza wydatek pola drenowego, a ∆ε określa zmianę intensywności infiltracji wywołaną
odprowadzeniem wód ściekowych do gruntu [na skutek odprowadzania wód ściekowych do gruntu
zmieni się transpiracja, parowanie z gleby, odpływ podziemny, a tym samym zmieni się również
intensywność infiltracji ε ].
Dla przyjętego schematu obliczeniowego stosujemy równanie Boussinesqa dla przypadku zagadnienia
osiowo – symetrycznego, równanie (7.21), którego rozwiązaniem jest uzyskana w poprzednim
podrozdziale funkcja:
2
2
.
+
1
ln +
'
1
,
(7.37)
funkcja:
'
,
'
1
=
=
=
warunków
brzegowych:
,
(7.39)
r
r
=1
z
Hr
dd
1
0
r
r
r
r
=1
Hr
dd
H
=
r
r
=1
=0
(7.38)
R
r
=0
H
1
.
wyznaczymy
r
1
'
H
1
ln +
H
,
2
+
C
r
r
Hd
Cd
C
C
C
,
ε
C
k
H
= −
Stałe
1
C
r
ε1
C
≤ ≤
r
k
H
= −
R
r
r
1
ln +
zwierciadło wody opisuje zatem funkcja:
1
a dla
+
C
r
1
C
0≤ ≤
2
2
r
r
Dla
r
k
H
ε
= −
=1
.
C
C
C
C
Wstawiając powyższe warunki brzegowe (7.39) do rozwiązań (7.37) i (7.38), otrzymujemy
układ 4 równań algebraicznych, z których wyliczamy stałe , ' , 1 , 1' :
C
ε
2
,
ε
2
1
2
2
−
+
ln 1 +
0
+
ε
2
2
−
R
+
−
2
1
C
0
ε1
R
k
=
2
2
1
H
C
'
ε1
−
H
r
R
C
C
r
k R
k
=
2
1
r
k
C
'
1
ε
r
k
=
r
k
= 0,
C
1
ln ,
(7.40)
ln .
Wstawiając powyższe stałe do (7.37) i (7.38), uzyskamy maksymalny poziom zwierciadła
wody przy czynnym polu drenowym. Pole drenowe musi być oczywiście założone powyżej
uzyskanego zwierciadła wody i odbierać założony wydatek wód ściekowych.
7.5 Szacowanie dopływu wody do odkrywek górniczych metodą wielkiej studni.
W górnictwie odkrywkowym do obniżenia zwierciadła wody zapewniającego ciągłość eksploatacji,
stosuje się bariery studni. Rozważmy dla przykładu odkrywkę z dwoma barierami studni: zewnętrzną i
wewnętrzną – rys. 31
Rys. 31. Schemat do obliczeń odkrywki z barierami studni (zewnętrzna i wewnętrzna).
r
Uzyskanie ścisłego rozwiązania w postaci zamkniętej jest dla barier studni nawet w stosunkowo
prostych warunkach hydrogeologicznych trudne, jeżeli nawet niemożliwe. Zadanie takie rozwiązuje się
metodami numerycznymi w oparciu o ogólne równanie Boussinesqa. Jedną ze stosowanych metod
obliczeń jest metoda wielkiej studni. Polega ona na tym, że odwadniany obszar obejmowany barierą
r
wewnętrzną sprowadza się do powierzchni kołowej o promieniu
odbywa się pobocznicą walca o promieniu
0
0
. Zakłada się ponadto, że dopływ
i ze jest to dopływ radialny. Przy tak poczynionych
założeniach, schemat obliczeniowy dopływu do wyrobiska, odpowiada schematowi dopływu do studni
– rys. 32
Rys. 32 Schemat obliczeniowy dopływu do wyrobiska
Korzystając z założeń poczynionych dla rozwiązania zagadnienia „wielkiej studni” należy określić:
R
Q
promień depresji R na podstawie wykresu 7.15,
dopływ do wyrobiska:
= πε
2
;
(7.41)
położenie zwierciadła wody w obrębie leja depresji:
2
0
)+ ε
H
rr
−
R
k
=
2
r
0
2
(
2
+
ln
2
0
,
(7.42)
0
F
r
przy czym
ε
r
k
H
= −
π
.
r
0
=η
b
a
Jeśli powierzchnia obejmowana barierą wewnętrzną jest zbliżona do kwadratu lub prostokąta:
+
4
,
a
b
gdzie:
a – długość wyrobiska,
b – szerokość wyrobiska,
η - współczynnik zależny od stosunku
(7.43)
zgodnie z tabelą 7.2.
ba
Tabela 7.2
η
0,0
0,2
0,4
0,6
0,8
1,0
1,0
1,12
1,16
1,18
1,18
1,18