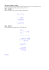Cieplo wlasciwe Cv gazu

Ciepło właściwe Cv gazu
Molowe ciepło właściwe Cv wodoru w zależności od temperatury. R – stała gazowa.
Ciepło właściwe wodoru w stałej objętości (Cv) zależy od temperatury i w różnych jej
zakresach przyjmuje wartości charakterystyczne dla:
- gazu jednoatomowego z trzema stopniami swobody (20-100 K),
- gazu dwuatomowego z 5 stopniami swobody (300-700 K),
- gazu dwuatomowego z 7 stopniami swobody (powyżej 3000 K).
Zależność ciepła właściwego od temperatury – dużo słabszą niż w przypadku wodoru –
wykazują także inne gazy, szczególnie w niskich temperaturach. Zmienność ciepła
właściwego wynika z kwantowania energii ruchu obrotowego i oscylacji (patrz: nast. strona).
Energia kinetyczna ruchu postępowego cząsteczek wodoru nie podlega kwantowaniu i
cząsteczki mogą ją posiadać w dowolnych ilościach, średnio po 3·(½kT). W niskich
temperaturach (20-100 K) stanowi jedyną formę energii cząsteczek i dlatego gaz wykazuje
ciepło właściwe 3R/2.
Energia ruchu obrotowego cząsteczek wodoru pojawia się w zakresie temperatur 100-300 K i
w tym zakresie ciepło właściwe wzrasta do wartości 5R/2, która odpowiada pięciu stopniom
swobody cząsteczek (3 dla ruchu postępowego oraz 2 dla obrotowego).
Energia oscylacyjna – kinetyczna i potencjalna – pojawia się w temperaturach 700-3000 K.
Oscylacjom wewnątrzcząsteczkowym towarzyszą duże porcje (kwanty) energii; wynika stąd
wzrost średniej energii cząsteczek o 2·(½kT) i wzrost molowego ciepła właściwego do 7R/2
(w cząsteczkach dwuatomowych) lub o większą wielokrotność tej wielkości.
1
Przykład: energia ruchu obrotowego cząsteczki wodoru
W cząsteczce wodoru jądra obu atomów krążą po okręgu o
d = 0,74 Å
promieniu (½)d wokół osi pionowej (patrz: rysunek obok).
Masa każdego z nich jest masą protonu mp . Energia kinetyczna cząsteczki wynosi:
oś
1 2
obrotu
E = Iω
2
Prawa mechaniki kwantowej stanowią, że moment pędu cząsteczki J:
J = Iω
(I – moment bezwładności cząsteczki)
nie jest dowolny, lecz stanowi wielokrotność stałej Plancka:
h
J = n⋅
= nℏ
(n = 0, 1, 2, 3, 4, ... )
2π
Wyznaczając prędkość kątową ω z tych dwu równań i podstawiając ją do E otrzymujemy:
n 2ℏ 2
E=
2I
Energia kinetyczna może zatem przyjmować wartości:
ℏ2
ℏ2
ℏ2
ℏ2
0,
, 4 , 9 , 16 , ...
2I
2I
2I
2I
Według zasady ekwipartycji energii średnia energia ruchu obrotowego ma związek z
temperaturą układu, którego część stanowi cząsteczka. Najmniejsza niezerowa ilość energii
(dla n = 1) może więc wystąpić w temperaturze spełniającej warunek:
ℏ2 1
≈ kT
2I 2
Traktując powyższy warunek jako równanie, po podstawieniu:
2
d
I = 2m p ⋅   = 4,6 ⋅ 10−48 kg ⋅ m 2
2
h
ℏ=
= 1,054 ⋅ 10 −34 J ⋅ s
2π
k = 1,38 ⋅ 10−23 J / K
otrzymujemy:
ℏ2
T=
= 176 K
kI
Jak widać na rysunku obok, jest to dość
dobre oszacowanie temperatury, w
której wyraźnie zaczyna pojawiać się
ruch obrotowy molekuł wodoru, a ciepło
właściwe osiąga wartość pośrednią
między 3R/2 i 5R/2.
W analogiczny sposób można otrzymać oszacowanie temperatury potrzebnej do wystąpienia
ruchu oscylacyjnego. Wynosi ona około 2000-3000 K (przejście od 5R/2 do 7R/2).
2