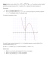RRZ (CSZ)

RRZ (CSZ)
1. Sformułowanie pojęcia klasycznego rozwiązania równania różniczkowego i
rozwiązania zagadnienia Cauchy’ego. Rozwiązanie ogólne. Przykład zagadnienia
Cauchy’ego bez jednoznaczności rozwiązania. Przykład równania z rozwiązaniami
uciekającymi do nieskończoności w skończonym czasie.

Sformułowanie pojęcia klasycznego rozwiązania równania różniczkowego i rozwiązania zagadnienia
Cauchy’ego.
Komentarz [pd1]: s.18
Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie
(
( )
̇ ̈
)
Wiążące zmienną niezależną t, zmienne zależne x i ich pochodne ̇ ̈
( )
aż do rzędu .
Rozwiązaniem równania nazywamy funkcję ( ) klasy ( ) , która podstawiona do równania w miejsce x (i
odpowiednio w miejsce ( ) w miejsce ( ) ) zmienia to równanie w tożsamość.
Wykres funkcji ( ) w przestrzeni
Równanie postaci (
( )
( )
( )
zmiennych (
( )
̇ ̈
̇( )
)
) nazywamy krzywą całkową równania.
można sprowadzić do równania pierwszego rzędu oznaczając
( )
( )
(
)
( ) i wprowadzając nową zmienną ̅ ( ) (
)
( )
( )
ostatecznie otrzymując ̇ ̅
(
(
̅)
̅)
( )
( )
(
(

)
)
Komentarz [pd2]: s. 21
Zagadnienie Cauchy’ego
Warunek postaci ( )
ograniczający zbiór rozwiązań równania pierwszego rzędu nazywa się warunkiem
początkowym (warunkiem Cauchy’ego). Równanie różniczkowe uzupełnione warunkiem Cauchy’ego
( ) ( )
̇
nazywa się zagadnieniem początkowym (zagadnieniem Cauchy’ego).
Rozwiązaniem zagadnienia początkowego nazywamy funkcję
spełniającą równanie ̇
( ) oraz warunek początkowy.
na przedziale [
( ) klasy
(
Jeśli dane jest równanie różniczkowe rzędu , postaci ( ) ( )
(
̇
zagadnienie początkowe (Cauchy’ego) dla tego równania przyjmuje formę:
( )

̇( )
(
)(
)
, gdzie
są wektorami
)
) w przestrzeni
(
̇
( )
],
(
, to
)
)
-wymiarowymi.
Rozwiązanie ogólne.
Jeśli (
(
)
parametry (
) jest rodziną funkcji sparametryzowaną parametrami
, taką, że dla każdego
)
(
) jest krzywą całkową równania i dla każdego (
istnieją
)
), to
, takie że (
) jest krzywą całkową przechodzącą przez punkt (
) nazywamy rozwiązaniem ogólnym równania.
rodzinę (
jest zbiorem spójnym w którym
( ) jest dobrze określona. Zbiór ten nazywany jest rozszerzoną przestrzenią
prawa strona równania ̇
fazową, a jego rzut D na przestrzeń
zmiennych – przestrzenią fazową tego równania.

Przykład zagadnienia Cauchy’ego bez jednoznaczności rozwiązania.
{

√| |
̇
( )
Przykład równania z rozwiązaniami uciekającymi do nieskończoności w skończonym czasie.
̇
2. Przykład zagadnienia Cauchy’ego bez rozwiązania. Przykład równania z
rozwiązaniami nieklasycznymi. Układy równań różniczkowych, równania
wyższych rzędów. Przejście od równania wyższego rzędu do układu równań
pierwszego stopnia.

{
̇
Przykład zagadnienia Cauchy’ego bez rozwiązania.
(
̇
)
( )
( )
{
dla

Przykład równania z rozwiązaniami nieklasycznymi.
(
)
{
Rozwiązanie nie istnieje w sensie formalnym; nie jest klasy

Układy równań różniczkowych
Komentarz [pd3]: s. 18-19

Równania wyższych rzędów.
Komentarz [pd4]: s. 18-19

Przejście od równania wyższego rzędu do układu równań pierwszego stopnia.
Komentarz [pd5]: s. 18-19
Równanie postaci (
( )
( )
(
.
( )
( )
( )
̇ ̈
( )
̇( )
) ostatecznie otrzymując ̇ ̅
)
można sprowadzić do równania pierwszego rzędu oznaczając
(
( )
(
)
( ) i wprowadzając nową zmienną (wektor)
( )
( )
̅ ), gdzie ( ̅ ) (
).
(
( )
)
3. Równania o zmiennych rozdzielonych. Wzór ogólny. Praktyczny sposób
znajdowania rozwiązań.
Analiza równania:
̇
̅( )

Komentarz [pd6]: s. 51-52
Równania o zmiennych rozdzielonych. Wzór ogólny.
( ) nazywamy równaniem o zmiennych rozdzielonych, jeśli funkcja dwóch zmiennych (
Równanie ̇
( )
jest iloczynem dwóch funkcji jednej zmiennej, tj. ( )
( )

)
Praktyczny sposób znajdowania rozwiązań.
( )
Dane jest równanie ̇
Komentarz [pd7]: s. 51
( )
( ), to dla każdego warunku początkowego
są ciągłe oraz ( )
dla
( ) zagadnienie Cauchy’ego ma jednoznaczne rozwiązanie. Krzywa całkowa
) jest dana wzorem: ( )
( )
( )), gdzie
równania przechodząca przez punkt (
( ( )
( ) jest funkcją pierwotną funkcji ( ), a ( ) – funkcją pierwotną funkcji
( ).
TW: Jeśli funkcja
( )
(
i
)
Dowód. Dane jest równanie ̇
( )
( ). Dzielimy je stronami przez
( ( ))
( ). Ta równość może zostać zapisana w postaci
funkcji
( ).
. Całkujemy ostatnie równanie w przedziale (
( )
jest funkcją monotoniczną, bo
( ) i otrzymujemy
( ) gdzie
) i otrzymujemy
, czyli pochodna
( )
( ) jest funkcją pierwotną
( ( ))
( ( ))
( )
ma stały znak. Istnieje więc funkcja
, odwrotna do . Korzystając z faktu, że ( )
możemy przekształcić poprzednie równanie do postaci
( )
( )
( )) otrzymując wzór z tezy twierdzenia. Mamy gwarancję, że otrzymane
( ( )
rozwiązanie jest jednoznaczne, bo całki oznaczone mają jednoznaczne wartości (funkcje pierwotne są
wyznaczone z dokładnością do stałej).

Analiza równania:
̇
̇
̇
(|
(punkt (
(
)
|)
(|
|)
(| |)
) jest punktem osobliwym tego równania)
|
|
| (
(
( )
(
)|
)
)
4. zapis równania w postaci różniczkowej.
Równania jednorodne. Twierdzenie o istnieniu rozwiązania dla równania
jednorodnego.
Analiza równania
(

)
Komentarz [pd8]: s. 61
Zapis równania w postaci różniczkowej.
Równanie różniczkowe w postaci różniczek zapisywane jest w następujący sposób:
(

)
(
)
Równania jednorodne.
Komentarz [pd9]: s. 62
Równanie różniczkowe w postaci różniczek nazywa się równaniem jednorodnym (stopnia ), jeśli funkcje
(
)i (
) są funkcjami jednorodnymi stopnia .
) nazywa się funkcją jednorodną stopnia n, jeśli (
Funkcja dwóch zmiennych (

)
(
)
Twierdzenie o istnieniu rozwiązania dla równania jednorodnego.
Komentarz [pd10]: s. 62
Dane jest równanie jednorodne stopnia n w postaci różniczek
(
O funkcjach
(
)i (
)
)
) zakładamy, że są funkcjami ciągłymi w zbiorze
(
Wtedy przez każdy punkt (

(
)
)
(
(
)
oraz
)
przechodzi dokładnie jedna krzywa całkowa równania.
Analiza równania
(
)
5. Równania zupełne.
(
Warunek na to, by wyrażenie
)
(
)
było różniczką zupełną.
Twierdzenie o istnieniu rozwiązania równania zupełnego (z dowodem).
Analiza równania
(

)
(
)
(
Równania zupełne. Warunek na to, by wyrażenie
)
(
)
Komentarz [pd11]: s. 66
było różniczką zupełną.
Komentarz [pd12]: s. 66
Niech dane będzie wyrażenie
(
I niech funkcje
(
), (
),
Jeśli w Q jest spełniona równość
(
)
(
),
(
),
(
)
(
)
) będą ciągłe w zbiorze
(
)
(
)
(
) .
To wyrażenie jest różniczką zupełną, czyli różniczką pewnej funkcji (
(
∫
)
(
)
). Wtedy również całka krzywoliniowa
,
Liczona po drodze L zawartej w Q nie zależy od drogi całkowania.

Twierdzenie o istnieniu rozwiązania równania zupełnego (z dowodem).
Zakładając, że w zbiorze
(
)
(
)
(
) funkcje M(
),
Komentarz [pd13]: s. 67
(
),
(
),
(
) są
ciągłe i spełniony jest warunek
(
)
(
),
Oraz jedna z funkcji M(
), (
) jest różna od zera w każdym punkcie zbioru Q. Wtedy przez każdy punkt
(
)
przechodzi dokładnie jedna krzywa całkowa równania
(
)
(
)
Dowód.
Załóżmy, że
(
)
. Wtedy równanie można przepisać w postaci
(
)
(
)
Ponieważ rozważamy różniczkę zupełną, więc istnieje taka funkcja (
(
)
(
), że
)
Wobec tego równanie można zapisać następująco
(
( ))
(
( ))
Rozwiązaniem tego równania jest

Analiza równania
(
)
(
)
Komentarz [pd14]: s. 68
(nie zależy od drogi całkowania)
6. Czynnik całkujący. Równanie opisujące czynnik całkujący.
Przypadek czynnika całkującego zależnego od jednej zmiennej.
Analiza równania
(

)
Czynnik całkujący. Równanie opisujące czynnik całkujący.
Komentarz [pd15]: s. 69
pomnożymy przez czynnik całkujący (
Jeśli wyrażenie
)
I zażądamy, żeby nowe wyrażenie było różniczką zupełną
To otrzymamy skomplikowane równanie o pochodnych cząstkowych
(
)
Często bywa tak, że równanie jest w pewnym sensie bliskie różniczce zupełnej. Wtedy czynnik
,
występujący po prawej stronie równania może być stały albo może być funkcją tylko jednej zmiennej. Sugeruje
to często poszukiwanie czynnika całkującego w postaci ( ), ( ), albo
( ), gdzie jest znaną funkcją
zmiennych i .

Przypadek czynnika całkującego zależnego od jednej zmiennej.
Przykład (
(
)
(
)
(
)
) zależne tylko od jednej zmiennej
równanie różniczki zupełnej; można całkować po dowolnej krzywej

Analiza równania
(
)
7. Definicja przestrzeni metrycznej, odwzorowania ciągłe między przestrzeniami
metrycznymi, warunek Lipschitza.
Ciągi spełniające warunek Cauchy’ego. Przestrzenie metryczne zupełne.
Twierdzenie o uzupełnianiu przestrzeni metrycznych.

Definicja przestrzeni metrycznej, odwzorowania ciągłe między przestrzeniami metrycznymi,
warunek Lipschitza.
Metryka (odległość)
Niech
będzie zbiorem niepustym. Metryką w zbiorze
nazywamy dowolną funkcję
spełniającą następujące warunki:
(i)
;
(ii)
(warunek symetrii);
(iii)
Parę
(warunek trójkąta).
nazywamy przestrzenią metryczną.
Dla dowolnych
oddalone od siebie o
liczbę
nazywamy odległością punktów i oraz mówimy, że punkty i są
Komentarz [pd16]: s. 349
(
)(
) – przestrzenie topologiczne. Odwzorowanie zbioru
( )
dowolnego zbioru
jego przeciwobraz
Niech
będą przestrzeniami metrycznymi. Mówimy, że
Lipschitza wtedy i tylko wtedy, gdy istnieje taka stała

nazywa się ciągłym, jeśli dla
spełnia warunek
, że dla dowolnych
Ciągi spełniające warunek Cauchy’ego.
Jeśli ciąg
punktów z przestrzeni metrycznej
(
)
.
Lemat: Ciąg
punktów z przestrzeni metrycznej
nazywa się ciągiem Cauchy’ego, jeśli jest spełniony warunek
zbieżny do punktu
jest ciągiem Cauchy’ego.
Przestrzenie metryczne zupełne.
Przestrzeń metryczna w której każdy ciąg Cauchy’ego ma granicę należącą do tej przestrzeni nazywa się
przestrzenią zupełną.

(
Twierdzenie o uzupełnianiu przestrzeni metrycznych.
) – przestrzeń metryczna.
Istnieje przestrzeń metryczna ( ̃ ̃ ) oraz odwzorowanie



̃ takie, że
Istnieje
(
) ̃
̃ ( ( ) ( ))
̃ jest granicą pewnego ciągu (
Każdy punkt ̃
( ̃ ̃ ) jest przestrzenią zupełną.
̃ o następujących własnościach:
(
)
)
( ( ) jest gęsty w ̃ )
8. Zasada Banacha. (z dowodem)
Tw. Niech będzie dana przestrzeń metryczna zupełna X i odwzorowanie
dla wszystkich
warunek
( ( ) ( ))
(
), gdzie
To istnieje dokładnie jeden punkt stały tego odwzorowania, tj. taki że ( )
Dowód.
. Jeśli odwzorowanie
.
spełnia
9. Twierdzenie Picarda-Lindelöfa o lokalnym istnieniu i jednoznaczności
rozwiązania zagadnienia Cauchy’ego – dowód oparty na Zasadzie Banacha.
Tw. Niech funkcja ( )
)|
czym
( ) | (
| (
)
(
)|
( ) |
|
będzie ciągła w zbiorze
oraz niech spełnia warunek Lipschitza względem zmiennej
|
|
|
, przy
w zbiorze , tj.
|,
Dla pewnej stałej L. Wtedy zagadnienie Cauchy’ego
(
̇
)
( )
Ma jednoznaczne rozwiązanie na przedziale |
|
(
).
Dowód. W dowodzie wykorzystamy twierdzenie Banacha o punkcie stałym (Zasada Banacha). W tym celu
rozważmy podzbiór przestrzeni metrycznej funkcji ciągłych
Łatwo zauważyć, że jako domknięty podzbiór przestrzeni funkcji ciągłych jest przestrzeniąmetrycznązupełną.
W przestrzeni rozważamy odwzorowanie
( )( )
∫
(
( ))
.
Jeśli istnieje punkt stały tego odwzorowania
( )
∫
(
( ))
,
To spełnia on równanie. Z ciągłości funkcji i własności całki wynikabowiem, że funkcja ( ) dana powyższym
równaniem jest funkcję różniczkowalną o ciągłej pochodnej. Po zróżniczkowaniu otrzymujemy równanie
(spełnienie warunku początkowego wynika z definicji całki). Wystarczy więc wykazać, że odwzorowanie ma
punkt stały w przestrzeni . W tym celu pokażemy najpierw, że odwzorowuje przestrzeń w siebie. Ze
względu na postać sprawdzenia wymaga jedynie warunek
| ( )( )
|
Mamy jednak
|
|
| ( )( )
|
|
|
|∫ (
( ))
|
|
|
∫
[
| (
]
( ))|
Komentarz [pd17]: str. 73
więc odwzorowuje przestrzeń
Wynika to z oszacowań
w siebie. Pokażemy obecnie, że
jest odwzorowaniem zawężającym.
[ oszacowania str. 74. TW. 3.5 ]
Tak więc dla
odwzorowanie jest zawężające. Z twierdzenia Banacha wynika, że ma punkt stały
tego odwzorowania w . Dowodzi to istnienia rozwiązania zagadnienia, a także jednoznaczności tego
rozwiązania.
10. Zbiory zwarte w przestrzeni metrycznej. Własności odwzorowań i funkcji
ciągłych określonych na zbiorze zwartym (jednostajna ciągłość, osiąganie
wartości najmniejszej i największej).

Zbiory zwarte w przestrzeni metrycznej.
Przestrzeń metryczną nazywa się przestrzenią zwartą, jeśli z każdego ciągu punktów
można wybrać
podciąg
zbieżny do pewnego
. Dowolny zbiór w przestrzeni metrycznej, spełniający powyższy
warunek nazywa się zbiorem zwartym.

Własności odwzorowań i funkcji ciągłych określonych na zbiorze zwartym (jednostajna ciągłość,
osiąganie wartości najmniejszej i największej).
11. Twierdzenie o istnieniu rozwiązań wysyconych będących przedłużeniem
dowolnie
przyjętego
rozwiązania.
(dowód
oparty
na
lemacie
Kuratowskiego-Zorna)
12. Twierdzenie o zachowaniu się rozwiązania wysyconego przy argumencie
zbieżnym do krańca dziedziny. (dowód na podstawie lematów, lematy bez
dowodu)
13. Porównanie rozwiązań dla równań, których prawe strony spełniają
nierówność. (z dowodem)
Warunek przedłużalności rozwiązania na całą prostą (z dowodem)

Porównanie rozwiązań dla równań, których prawe strony spełniają nierówność. (z dowodem)

Warunek przedłużalności rozwiązania na całą prostą (z dowodem)