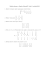Materiały pomocnicze do ćwiczeń z rachunku wektorowego i

RACHUNEK WEKTOROWY I ELEMENTY ALGEBRY LINIOWEJ
Dla studentów kierunku In»ynieria Bezpiecze«stwa
Materiaªy pomocnicze do ¢wicze«
Liczby zespolone
I
Wykona¢ nast¦puj¡ce dziaªania:
II
Znale¹¢ liczby
2 − 3i
1.
5 + 4i
√
√
2.
( 2 + i)(3 − 3i)
rzeczywiste x, y speªniaj¡ce równanie
x(2 + 3i) + y(4 − 5i) = 6 − 2i
1.
1 + yi
= 3i − 1
x − 2i
3.
(2 + yi)(x − 3i) = 7 − i
9 − 2i
x + yi
=
4.
x − yi
9 + 2i
2.
III
W zbiorze liczb zespolonych rozwi¡za¢ równanie
z 2 − 4z + 13 = 0
1.
2.
(1 + i)z + 3(z − i) = 0
z 2 = −4z̄
z+1
= −1
z̄ − 1
3.
4.
IV
Liczb¦ zespolon¡ zapisa¢ w postaci trygonometrycznej
√
3−i
1.
1+i
π
π
3.
sin + i cos
3
3
π
4.
1 + itg
3
2.
V
Obliczy¢ warto±¢ wyra»enia. Wynik zapisa¢ w postaci algebraicznej
1.
2.
3.
√
( 3 − i)10
(i − 1)8
π
π
cos − i sin
4
4
!10
2
Katarzyna Doma«ska, AJD Cz¦stochowa
(i + 1)22
√
(1 − i 3)6
4.
VI
Wyznaczy¢ pierwiastki zespolone
√
4
z, gdzie z = −4
√
4
2.
z, gdzie z = −i
√
3
3.
z, gdzie z = i
√
z, gdzie z = −11 + 60i
4.
√
5
z, gdzie z = 32i
5.
1.
VII
Wyznaczy¢ pierwiastki równania
z 4 = (1 − i)4
(z − i)4 = (z + i)4
3
Katarzyna Doma«ska
Rachunek macierzowy


I.
dla
Na podanych parach macierzy
i ∈ {1, 2, 3, 4, 5, 6, 7}

A5 = 

Ai , Bi
wykona¢ dziaªa-
nie mno»enia w takiej kolejno±ci, w jakiej
jest ono wykonalne.
"
B5 =
A6 =
−1 −1 −1 1
−1 −1 2 0 


−1
3
0 0 
4
0
0 0

A1 =






B1 = 


1
0 −1 2
2
1
0 −1 


−1 2
1
0 
0 −1 2
1



1 2 2


A2 =  2 1 0 
1 1 1
"
B2 =
"
1 1 2
1 0 1
#
#
3 −1 2 0
−2 −3 1 4
A3 =


B3 = 




A4 = 






B4 = 
1
2
1
1
1
3
1
1
2
−1
−1
1
2
1
1
1
1
1
0
0
3
4
1
2
2
0
2
1
2
0
1
1





1
2
1
0
−1
−2
−1
−2










B6 =
A7 =





1 2 2
0 1 2
"
"
2
2
1
1
1 1 2 −1
1 0 1 −2
"

1
2
2
1
1 2
0 1
#
#
1 2 3 0
0 1 2 1




B7 = 
1
0
1
0
2
2
3
1
#
1
4
2
0





#
4
Katarzyna Doma«ska, AJD Cz¦stochowa
II.
Obliczy¢ wyznaczniki podanych
macierzy kwadratowych.
2
1 −1 3 4
−1
−1
1 −1 1 
Y =


1
0
0
2 5


1 0 0

X= 5 2 1 

3 1 1


Z=

2 3 4


Y =  5 −2 1 
1 2 3




Z=




U =




A=


C=


III.
3
1
3
2
2
2
1
0
1
0
2
1




1
1
1
1
1 −1 1
1
1
1 −1
1
1
1
1 −1




0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0








1 2 1


X= 1 0 2 
0 1 0
1
1
4
1
3
1
1
1
1
5
4
1













2 −1 3 −2 4


B =  4 −2 5 −2 7 
2 −1 1 8 2








C=









Wyznaczy¢ rz¡d dla podanych ma-

1
3
1
1
2
1
−1 2 0 1


A =  1 3 −2 4 
1 0 −3 1

0 9
1
5
1 2
1
7
2 −4 −1 −5
1 2
1
0
cierzy.









2
1
1
1
1
1

1
2 3 0
0 −4 1
2
9 −6 0
3
1 −2 1 −1

B=
1
1
2
0


1 3
5 −1
2 −1 −3 4 


5 1 −1 7 
7 7
9
1

5
Katarzyna Doma«ska
IV.
Ukªady równa«
Znale¹¢, o ile istniej¡, macierze od-
wrotne do podanych.

I.

1 2 3


X= 2 3 4 
3 4 1
Rozwi¡za¢ nast¦puj¡ce ukªady rów-
na«:


1 1 −1
1
0 
Y =

 2
1 −1
1
1.



x + y − 2t = 0
x − y − 2z = 2

 3x + y − 2z − 4t = 2


1 2 −3

2 
Z= 0 1

0 0
1

2.

2
2 3

U =  1 −1 0 

−1
2 1
1 2 3


A= 0 2 3 
0 0 3


2
5
7

6
3
4 
B=

5 −2 −3

C=



D=




1
−1
1
0
x + 3y − 4z = 4
3x + 2y − z = 1

 x − 4y + 7z = 5
3.





2x + y − z + t = 5
x + y + z − 2t = −1
4.

x − 2y + z + t = 2



x+z =3

1 −3 −1
−2
7
2 

3
2 −4
1
2
4
0
1
1
1
0
0
0
0
3





x + 3y = 10
3x − y = 8

 x − 7y = −2








5.



2x + 3y + z = 3
4x + 6y + 2z = 1

 6x + 9y + 3z = 2



x − y + 2z − t = 2
2x − 3y − z + t = 1
6.

 x + 7z − 4t = 5
6
Katarzyna Doma«ska, AJD Cz¦stochowa
II.
Rozwi¡za¢ nast¦puj¡ce ukªady rów-
na« (przykªady poni»sze pochodz¡ ze zbioru zada« J. Sikorska, Zbiór zada« z matematyki dla studentów chemii, Wyd. U‘, Ka-
10.



5x + 4y − 2z + 3t = 2
3x + 2y − 6z + 9t = 4

 4x + 3y − 4z + 6t = 3
towice 2002):






x + 3y = 5
1.  3x − y = 4
 x − 7y = −1
(
2.
x − 2y + 5z = 0
2x − y + z = 1



x−y+z =1
−x + y − z = −1

 2x − 2y + 2z = 2
3.
(
x + 2y − 3z + t = 1
3x + 6y − 9z + 3t = 0
4.



x − y + 2z = −3
5.  −x + 2y − z = 5
 2x + y − z = 8



3x − 2y + 3z = 2
x − y + 2z = 0

 5x − 3y + 4z = 4
6.



x + y − 2t = 0
x − y − 2z = 2
7.

 3x + y − 2z − 4t = 2





−3x + y + z = −1
−2x + 2y + z = 1
8. 
x+y+z =3



−3x + y + 2z = 1





x + 2y − t = 1
−x + 3y − z − 3t = 2
9.

3x + y + z + t = 0



2x − y + z + 2t = −1
2x − 3y + 5z + 3u = 0
11.  4x − y + z + u = 0
 3x − 2y + 3z + 4u = 0



x − 2y + 3z = 0
4x + 7y + z = 0

 3x + 6y + 7z = 0
12.



x + 2y + 3z = 6
2x + y + z = 4
13.

 3x + y − 4z = 0



2x − y − 5z = 0
14.  3x + 4y − 2z = 11
 3x − 2y + 4z = 11
15.



2x + y + z = 1
x−y+z =0

 4x − y + 3z = 1



x+y−z =4
16.  3x − 2y − z = 0
 2x + y + 2z = 2
17.



x + 2y + 3z = 5
x + 3y + 4z = 6

 2x − y − z = 1





2x − y + z − 3t = 7
x + y − 2z + t = 1
18.

2y − 5z + t = 3



x − 3y + 2z − t = 1





5x − y + z − 2t = 3
4x − 2t = 5
19. 
5x + y − z + 2t = −1



7x − t = 3