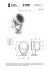Ćwiczenie 5 - Co i gdzie?

Pracownia elektryczna i elektroniczna. Elektronika cyfrowa.
Klasa III
Ćwiczenie nr 5.
Opracuj projekt realizacji prac związanych z badaniem działania cyfrowych
bloków
arytmetycznych
realizujących
operacje
sumowania
(sumatory)
i
porównywania (komparatory), oraz badaniem działania rejestrów cyfrowych. Zrealizuj
projekt.
Opracuj wyniki badania: półsumatora i sumatora 1-bitowego, pojedynczego
sumatora scalonego 7483, pojedynczego sumatora scalonego 7483 realizującego
funkcję odejmowania, łączenia dwu sumatorów 7483, komparatora scalonego 7485,
łączenia dwu komparatorów 7485, scalonego rejestru równoległego 74175 i (lub)
7475 oraz scalonego rejestru szeregowego 74194. Podczas badania zwróć
szczególną uwagę na zmiany stanów logicznych badanych elementów i ich
zgodność z zapisami katalogowymi.
Podczas pomiarów dostępne są:
- uniwersalne stanowisko laboratoryjne, umoŜliwiające zamontowanie 3 dowolnych
układów scalonych do 20 nóŜek, posiadające zasilacz prądu stałego 5V,
regulowany zasilacz prądu stałego 1,2-12V, zestaw kontrolnych diod LED, zestaw
przełączników umoŜliwiających zadawanie poszczególnych stanów logicznych.
- stanowisko do badania sumatorów i komparatorów.
- zestaw podstawowych bramek logicznych oraz układów scalonych (sumatory,
komparatory i rejestry) wskazanych do badania.
Projekt realizacji prac poprzedź informacjami o charakterze „danych” do
rozwiązania zadania, wynikającymi z analizy treści zadania i załączników.
Projekt realizacji prac powinien zawierać:
•
wykaz działań związanych z badaniem sumatorów, komparatorów i rejestrów,
•
schematy układów pomiarowych do badania sumatorów, komparatorów i
rejestrów,
•
opis sposobu pomiarów funkcji logicznych realizowanych przez badane
sumatorów, komparatorów i rejestrów,
•
wskazania eksploatacyjne dla uŜytkownika badanych sumatorów, komparatorów i
rejestrów, wynikające z załoŜonych warunków technicznych dotyczących
zasilania, obciąŜenia oraz warunków środowiskowych wymaganych podczas ich
działania.
Strona 1 z 13
Dokumentacja z badania sumatorów, komparatorów i rejestrów powinna
zawierać:
•
tabele funkcji arytmetycznych realizowanych w oparciu o badane sumatory i
zestawy sumatorów dla kilku wybranych liczb (min. 5), wraz z porównaniem z
wynikami teoretycznymi,
•
tabele porównania kolejnych liczb 4-bitowych podawanych w takiej konfiguracji,
aby bity, poczynając od najbardziej znaczących w dół najpierw były przeciwne, a
następnie równe sobie. Uwzględnić stany wejść kaskadowych z poprzedniego
komparatora,
•
tabele porównania kilku (min. 3) liczb 8-bitowych,
•
tabele funkcji realizowanych w oparciu o badane rejestry dla kilku wybranych liczb
(min. 5), wraz z wynikiem przesunięcia dla rejestru szeregowego,
•
wnioski
z
porównania
wyników
badań
z
załoŜeniami
teoretycznymi
(katalogowymi).
Do wykonania zadania wykorzystaj:
Załącznik 1 – Przykładowe operacje na liczbach binarnych.
Załącznik 2 – Topografia wyprowadzeń uŜytych układów scalonych.
Załącznik 3 – Zasady działania i zastosowania wybranych cyfrowych bloków
arytmetycznych.
Załącznik 1 – Przykładowe operacje na liczbach binarnych.
Zapis liczb w formacie binarnym:
27
26
25
24
23
22
21
20
128
64
32
16
8
4
2
1
Liczbę moŜna podzielić na:
cyfra bardziej znacząca
8
4
2
cyfra mniej znacząca
1
8
Strona 2 z 13
4
2
1
Odejmowanie
Zmiana znaku:
Przeprowadzamy poprzez negację i
dodanie 1
+/-
11001101
=
+
=
00110010
00000001
00110011
-
=
01001101
10011100
(A)
(B)
Zamiast odejmować, dodajemy
zanegowaną liczbę i 1:
+
+
Dodawanie
+
01000110
00110100
001000110
011001011
000000001
(A)
100010010
=
EXOR (dodawanie modulo 2)
(A)
(B)
⊕
=
11101001
01101111
10001010
11100101
Załącznik 2 – Topografia wyprowadzeń uŜytych układów scalonych.
Sumator UCY 7483N
Układ UCY 7483N jest monolitycznym układem scalonym średniej skali integracji.
Jest to 4- bitowy sumator dwójkowy, równoległy, z przeniesieniem równoległym. Sumator
ma wejścia sumy z kaŜdego bitu oraz wyjście przeniesienia (C4) z ostatniego bitu.
Rys.2.1 Schemat wejść i wyjść układu UCY 7483
Strona 3 z 13
Komparator UCY 7485N
Układ jest monolitycznym układ scalonym, który stanowi komparator wielkości
dwóch liczb dwójkowych, 4- bitowych z moŜliwością ich porównania i określenia, która jest
większa. Komparator ten posiada wejścia liczb porównywanych: A3, A2, A1, A0, B3, B2,
B1, B0 oraz wejścia i wyjścia kaskadowe: A>B, A=B, A<B, które umoŜliwiają tworzenie
układów porównujących liczby więcej niŜ 4- bitowe.
Rys. 2.2 Schemat wejść i wyjść układu UCY 7485
Strona 4 z 13
Rejestr przesuwny UCY 74194
Rys.2.3 Schemat wejść i wyjść układu UCY 74194
Układ jest 4-bitowym rejestrem przesuwnym z moŜliwością równoległego wpisywania
danych. Wejścia A, B, C, D (X0-X3) są wejściami równoległymi danych. Wyjścia QA, QB, QC,
QD (Q0-Q3) są wyjściami danych. Wejścia S0 i S1 słuŜą do ustawiania stanu pracy rejestru.
Wejścia SR (XP) i SL (XL) słuŜą odpowiednio jako wejścia bitu ostatniego i pierwszego przy
przesuwaniu w prawo lub w lewo. Wejście CLK (C) słuŜy jako wejście taktujące działanie
rejestru. Wejście CLR (R) jest nadrzędnym wejściem zerującym rejestr.
Rejestr równoległy UCY 74175
Rys.2.4 Schemat wejść i wyjść układu UCY 74175
Strona 5 z 13
Rejestr równoległy UCY 74175
Rys.2.5 Schemat wejść i wyjść układu UCY 7475
Załącznik 3 – Zasady działania i zastosowania wybranych cyfrowych bloków
arytmetycznych.
a) Sumatory
Sumator jest cyfrowym układem kombinacyjnym, co oznacza, Ŝe stan jego wyjść
zaleŜy jedynie od stanu wejść. Sumator wykonuje arytmetyczną operację dodawania dwóch,
lub więcej liczb binarnych. Logika operacji w sumatorze 1-bitowym przedstawiona jest w
tabeli poniŜej:
Ai Bi Si Ci+1
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Suma S i przeniesienie C dodawania jednobitowych liczb dwójkowych A i B
Zmienna Si reprezentuje rezultat operacji, jej wartość jest sumą modulo 2 (exclusive OR)
składników Ai, Bi i Ci. Zmienna Ci reprezentuje przeniesienie
z pozycji młodszej sumatora wielopozycyjnego. Ci+1 jest przeniesieniem do pozycji starszej.
Ci nie występuje w tzw. półsumatorze, obecność Ci daje sumator pełny. Z wartości
przedstawionych na rys. 11.1 moŜna określić wyraŜenia logiczne dla półsumatora:
- suma Si = Ai-Bi + ~AiBi = Ai (+) Bi,
- przeniesienie Ci+1 = AiBi.
Strona 6 z 13
Półsumator
Półsumator pozwala nam na dodanie dwu jednobitowych liczb binarnych Ai oraz Bi.
b)
a)
Rys.3.1 Schemat półsumatora: a) ideowy b) blokowy
Sumator
Sumatory dzielimy na:
a.
dwójkowe, gdzie działania wykonuje się na liczbach dwójkowych,
b.
dziesiętne, wykonujące działania na liczbach dziesiętnych kodowanych
dwójkowo.
Gdy za kryterium podziału przyjmuje się sposób podawania składników sumy, wtedy
moŜna wyróŜnić sumatory:
c.
d.
równoległe:
•
z przeniesieniem szeregowym,
•
z przeniesieniem równoległym,
szeregowe.
W pracy wykorzystane są dwa sumatory czterobitowe z moŜliwością połączenia ich w szereg,
co pozwala uzyskać sumator ośmiobitowy.
Strona 7 z 13
Rys. 3.2 Sumator dwuargumentowy jednobitowy
Łączenie sumatorów
Sumator kaskadowy n-bitowy jest układem powstałym przez połączenie n sumatorów
jednobitowych. Schemat blokowy takiego sumatora przedstawiono na rysunku 3.3. Przy
sumowaniu liczb dodatnich wejście przeniesienia początkowego C0 nie jest wykorzystywane
(C0=0, dla pewności naleŜy podpiąć wejście to do szyny z sygnałami logicznymi „0”).
Rys. 3.3 Schemat blokowy sumatora kaskadowego.
W sumatorze kaskadowym wszystkie cyfry dodawanych liczb dwójkowych podawane
są na sumator jednocześnie. Czas uformowania się wyniku zaleŜy od prędkości propagacji
sygnału przeniesienia przez kolejne komórki sumatora. W najbardziej niekorzystnym
przypadku sygnał C musi przejść przez wszystkie komórki sumatora. Czas sumowania moŜna
znacznie skrócić przez zastosowanie sumatora z równoległym przeniesieniem. Sumator z
przeniesieniem równoległym generuje wszystkie wartości przeniesień jednocześnie na
podstawie wartości na poszczególnych bitach obu operandów.
Przeniesienie Ci+1 = AiBi + AiCi + BiCi = AiBi + (Ai+Bi)
Strona 8 z 13
Ci moŜna wyrazić w postaci: Ci+1= Gi+TiCi, gdzie: Gi=AiBi, Ti=Ai+Bi.
Dla modułu czterobitowego i <{0,1,2,3}:
C4=G3+T3G2+T3T2G1+T3T2T1G0+T3T2T1T0
lub C4 = G + TC0,
gdzie G= G3+T3G2+T3T2G1+T3T2T1G0; T=T3T2T1T0,
gdzie:
G - przeniesienie generowane w bloku,
T - sygnał warunkujący transmisję przeniesienia początkowego C0.
WyraŜenie dla sumy: Si = Ai (+) Bi(+)Ci moŜna przekształcić do postaci:
Si = Ci(+)~(AiBi)(Ai+Bi)= Ci (+) ~GiTi.
b) Komparatory
Komparatorem najprościej moŜna nazwać układ do porównywania dwóch liczb. W
układach cyfrowych wykorzystywane są komparatory porównujące dwie liczby binarne.
Wynikiem porównania liczb A i B moŜe być jedna z trzech relacji: A=B, A>B, A<B.
Niekiedy wystarczy jedynie komparator pozwalający na odróŜnienie relacji: A=B i A≠B lub
np. A≤B i A>B. Najprostszym komparatorem jest układ porównujący poziomy napięć na
dwóch wejściach. Typowym jednak komparatorem jest układ 7485, który umoŜliwia
porównanie dwóch liczb 4-bitowych.
Rys.3.4 Schemat wejść i wyjść komparatora 4-bitowego
Łączenie komparatorów
Komparator scalony 7485 posiada 3 wyjścia: ”A=B”, „A>B”, „A<B”. Na jednym z
nich pojawia się poziom logiczny „1”, określający zaleŜność między dwoma czterobitowymi
Strona 9 z 13
słowami wejściowymi A i B. Układ ma ponadto 3 wejścia oznaczone identycznie jak wyjścia:
”A=B”, „A>B”, „A<B”. SłuŜą one do współpracy z innymi układami scalonymi 7485 w celu
porównywania liczb o długości większej niŜ czterobitowa. Wejścia te naleŜy wówczas
połączyć z odpowiadającymi im wyjściami komparatora młodszych bitów. Przy takim
łączeniu komparatorów waŜne jest, aby w komparatorze najmłodszych bitów lub pracującym
pojedynczo była zapewniona następująca kombinacja sygnałów wejściowych: (A=B)=1,
(A>B)=0, (A<B)=0.
Rys.5 Łączenie dwóch komparatorów 4-bitowych
c) rejestry
Rejestry moŜemy podzielić na: równoległe i przesuwające.
Rejestry równoległe.
Rejestr równoległy słuŜy do przechowywania (pamiętania) pojedynczego słowa
binarnego. Zasadniczą mikrooperacją wykonywaną na rejestrze jest wpisanie słowa
wejściowego X do rejestru. Mikrooperację tą moŜemy zapisać:
Y:=X
gdzie Y – wyjście, na którym pojawia się przechowywane w rejestrze słowo. W niektórych
rejestrach moŜliwa jest teŜ operacja zerowania zawartości rejestru (Y:=0).
Rejestr równoległy moŜe być zbudowany z przerzutników złoŜonych lub prostych.
Przepisanie wejścia rejestrów na ich wyjścia następuje po pojawieniu się stanu wysokiego na
wejściu L (ładuj). W zaleŜności od typu rejestru, stan wejściowy jest przekazywany na
Strona 10 z 13
wyjście tylko podczas narastania sygnału L (zbocze narastające) (74175) lub teŜ podczas
całego trwania stanu wysokiego wejścia L (7475-rejestr zatrzaskowy).
Rys. 3.6. Rejestr równoległy 74175
Rys. 3.7. Rejestr równoległy 7475
Rejestry przesuwające:
Rejestr przesuwający realizuje przesunięcie zapamiętanego w nim słowa o jedną
pozycję w lewo lub prawo. Mikrooperacja przesunięcia w lewo polega na jednoczesnym
wpisaniu do kaŜdego przerzutnika Qi stanu poprzedniego przerzutnika Qi-1. Do pierwszego
Strona 11 z 13
przerzutnika (Q0) zostaje wpisany sygnał wejściowy XL, a zawartość ostatniego przerzutnika
(Q3 – na rys.) jest tracona.
Q0:=XL
Q1:=Q0
Q2:=Q1
Q3:=Q2
Mikrooperacja przesunięcia w prawo polega na jednoczesnym wpisaniu do kaŜdego
przerzutnika Qi stanu następnego przerzutnika Qi+1. Do ostatniego przerzutnika (Q3 – na rys.)
zostaje wpisany sygnał wejściowy XP, a zawartość pierwsego przerzutnika (Q0) jest tracona.
Q0:=Q1
Q1:=Q2
Q2:=Q3
Q3:=XP
Rejestry przesuwające są realizowane w wielu wersjach. W niektórych z nich jest
moŜliwy równoległy zapis danych, a następnie ich przesuwanie w prawo lub w lewo (74194).
Kierunek przesuwania moŜe być zadawany w nim wejściami S0 i S2.
S1
S0
0
0
przesunięcie w prawo
0
1
przesunięcie w lewo
1
0
wpisywanie Q:=X
1
1
pamiętanie
Czynność
Rys. 8. Rejestr przesuwający.
Rys. 3.9 Operacja przesunięcia w prawo
Strona 12 z 13
Rys. 3.10. Rejestr przesuwający dwukierunkowy 74194
Rys.3.11. Typy rejestrów przesuwających
Strona 13 z 13