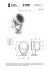Konsolidacja torfów z wykorzystaniem przeciążenia warstwą popiołów

Konsolidacja torfów z wykorzystaniem przeciążenia warstwą popiołów
prof. dr hab. inż. Zygmunt Meyer
Zachodniopomorski Uniwersytet Technologiczny w Szczecinie, Katedra Geotechniki
al. Piastów 50, 70-310 Szczecin
dr inż. Tomasz Szczygielski
Ekotech Sp. z o.o. ul. Niedziałkowskiego 47A/4, Szczecin
WSTĘP
Rozwój urbanistyczny kraju powoduje, że przy podejmowaniu kolejnych inwestycji
coraz częściej jesteśmy zmuszani do posadawiania obiektów budowlanych na gruntach
słabych. Przykładem są obszary torfowe, które zalegają najczęściej w sąsiedztwie rzek i
zalewów i są atrakcyjnymi miejscami z uwagi na wykorzystanie transportu wodnego.
Praktyka inżynierska dowodzi, że tereny na których występują grunty słabe można wzmocnić
wykorzystując zjawisko konsolidacji.
Grunty słabe charakteryzują się dużymi osiadaniami przy niewielkich obciążeniach
np. przy miąższości torfów 6 m osiadanie może wynosić 1,5 ÷ 2,0m. Jest to związane z
małym modułem ściśliwości tego gruntu organicznego. Konsolidacja tych gruntów poprzez
wykonanie warstwy przeciążającej powoduje wzrost modułu ściśliwości z wartości
początkowej ok. 300 kPa do nawet 2 MPa. Taki moduł pozwala na zaprojektowanie
posadowienia bezpośredniego dla obiektów o niedużych naciskach: drogi, place składowe,
place manewrowe oraz niewysokie obiekty budowlane [7]. Do wykonania warstwy
przeciążonej wykorzystuje się często grunt mineralny co wiąże się z degradacją środowiska
związaną z pozyskaniem tego materiału. Można również wykorzystać urobek z dna akwenów
pochodzący z pogłębienia. Skażenie wód powierzchniowych powoduje, że materiał ten
traktowany jest jako odpad, który przed wbudowaniem powinien ulec przeróbce. Mając na
względzie znaczne obszary, które można poddać procesowi wzmocnienia przez konsolidację,
w niniejszej pracy proponuje się do wykonania warstwy przeciążającej wykorzystać uboczny
produkt spalania węgla w elektrowniach (materiał odpadowy) czyli popiół. Popiół pod
względem własności geotechnicznych odpowiada frakcji pyłowej przy czym posiada on
wysoki kat tarcia wewnętrznego nawet 40o, natomiast współczynnik filtracji tych utworów
antropogenicznych jest bardzo mały ok. 10-7 m/s. Ten mały współczynnik filtracji powoduje,
że w procesie konsolidacji odpływająca filtracyjnie na zewnątrz woda gruntowa nie jest
odbierana przez warstwę przeciążającą, tak jak to ma miejsce w przypadku przeciążania
warstwą piasku. W przypadku przeciążenia piaskiem główny kierunek filtracji wody
gruntowej występuje w kierunku pionowym do góry, gdzie woda jest odbierana przez piasek.
Przypadek taki został opisany w literaturze przez Terzaghiego [8]. W przypadku, kiedy
warstwa przeciążająca jest wykonana z popiołów i nie odbiera wody gruntowej, filtracja może
się odbywać jedynie w kierunku poziomym do krawędzi składowiska. Można oczekiwać, że
ponieważ poziome wymiary obszaru konsolidowanego są wielokrotnie większe niż miąższość
warstwy torfów, dlatego też czasy konsolidacji będą dłuższe.
Przedmiotem niniejszej pracy jest analiza mechanizmu konsolidacji w przypadku, gdy
przeciążenie popiołami wymusza poziomy kierunek filtracji wody gruntowej w
konsolidowanej warstwie torfu. Zakres pracy obejmuje matematyczny opis zjawiska
konsolidacji torfów przeciążonych warstwą popiołów oraz weryfikację tego modelu w
oparciu o badania terenowe wykonane na poligonie doświadczalnym o powierzchni ok. 10 ha
w miejscowości Skolwin k/Szczecina (Szczygielski) [5].
OPIS MATEMATYCZNY KONSOLIDACJI WARSTWY TORFU
PRZECIĄŻONEJ POPIOŁAMI
Model fizyczny rozpatrywanego procesu konsolidacji zakłada, że przeciążona warstwa
torfu stanowi ośrodek porowaty, który wypełniony jest wodą. Pod wpływem obciążenia
zewnętrznego następuje ściskanie kolumny tego gruntu i osiadanie. Osiadanie jest możliwe po
uwolnieniu części porów gruntowych na skutek filtracyjnego odpływu wody. do opisu filtracji
przyjmuje się prawo Darcy przy czym współczynnik filtracji zmienia się w trakcie
konsolidacji. Osiadanie kolumny gruntu pod wpływem obciążenia wynika z jednoosiowego
stanu naprężeń – osiadań w kierunku pionowym
Zakładamy, że moduł ściśliwości może się zmieniać wraz ze zmniejszaniem się
porowatości na skutek poziomego filtracyjnego odpływu wody. Zakładamy, że w kierunku
pionowym własności fizyczne gruntu nie zmieniają się wobec braku filtracji pionowej.
Zakładamy też, że torf spoczywa na warstwie gruntu podścielającego, który jest
nieodkształcony (duży moduł ściśliwości) oraz że nie występuje w nim filtracja wody.
Szczegółowo model fizyczny przedstawiono w poprzednich opracowaniach [3,4,6]. Schemat
przedstawiono na rys. 1.
z
Warstwa nasypowa
H
u(x)
H
u(x+dx)
dz
Warstwa
konsolidowana
0
Warstwa
nośna
x
x+dx
x
Rys. 1 Schemat geometryczny konsolidowanego obszaru [5 ]
Dla tak przyjętych warunków ciągłość przepływu wody wyraża równanie:
kx
∂ 2u
∂ 2 u γ w ∂u
+
k
=
⋅
y
∂x 2
∂y 2 Me ∂t
(1)
W równaniu tym k x oraz k y oznaczają współczynnik filtracji wody w torfie w płaszczyźnie
poziomej, Me - jest edometrycznym modułem ściśliwości torfu w kierunku pionowym, u –
jest ciśnieniem porowym, x,y - są osiami głównego układu współrzędnych, który znajduje
się w płaszczyźnie poziomej, oś z - jest osią pionową, natomiast γ w - jest ciężarem
2
objętościowym wody. Można wykazać, że całkę ogólną równania (1) dla obszaru
prostokątnego o dwóch osiach symetrii można wyrazić iloczynem dwóch funkcji o
rozdzielonych zmiennych. Mamy
(2)
u(x, y, t) = F1(x, t) · F2(y, t)
Funkcje F1 oraz F2 są rozwiązaniem poniższych równań
kx ⋅
∂ 2 F1 γ w ∂F1
=
⋅
∂x 2 Me ∂t
;
ky ⋅
∂ 2 F2 γ w ∂F2
=
⋅
∂y 2
Me ∂t
(3)
Warunki brzegowe rozwiązania ustalamy następująco (rys. 2)
dla x = ±
L
;
2
u=0
oraz F1 = 0
B
; u = 0 oraz F2 = 0
2
Ponadto z uwagi na symetrię obszaru rozwiązania mamy
dla y = ±
∂u
=0
∂x
∂u
dla y = 0
=0
∂y
dla x = 0
oraz
(4)
(5)
(6)
(7)
Rys. 2 Warunki brzegowe przyjęte do rozwiązania[5 ]
3
Z badań filtracji przeprowadzonych przy zastosowaniu teorii ruchu potencjalnego
wynika, że w praktyce zanikanie ciśnienia porowego na brzegu obszaru nie następuje
bezpośrednio na krawędzi tak jak to opisano wzorami (4) i (5), ale w pewnej odległości δ .
Badania te wskazują, że za wartość δ można przyjąć miąższość warstwy torfów czyli
δ = H . Jako warunek początkowy przyjęto
dla t = 0 u(x,y,z) = const = σo
(8)
gdzie: σo - jest obciążeniem zewnętrznym wywołanym przez warstwę przeciążającą . Ponadto
żądamy żeby był spełniony warunek
lim u = 0
(9)
t →∞
co oznacza monotoniczne zanikanie ciśnienia wody w porach gruntowych.
Dla tak przyjętych warunków brzegowych i początkowych z uwagi na symetrię układu
funkcji F1 oraz F2 mają postać:


2
 2 

 1

1
x' 
1
F1 ( x ,t ) = ⋅ ∑ 
⋅ sin  n +  ⋅ π ⋅  ⋅ exp − π ⋅  n +  ⋅ 4τ x  
π n=o  n + 1
2
L' 
2



 

2

2
gdzie:
∞
L’ = L + H ;
x' =
τx =
t
;
Tox
L
−x
2
 L' 
γw ⋅ 
2
Tox =
k x ⋅ Me
2
(11)
oraz
(12)


2
 2

 1

1
y' 
1
F2 ( y ,t ) = ⋅ ∑ 
⋅ sin  n +  ⋅ π  ⋅ exp − π  n +  ⋅ 4τ y  
π n=o  n + 1
2  B' 
2



 

2

2
gdzie:
(10)
∞
B’ = B + H ;
τy =
t
;
Toy
 B' 
γw ⋅ 
2
T oy =
k y ⋅ Me
B
−y
2
Rozwiązanie równania wyjściowego (1) ma postać:
(13)
2
(14)
y' =
(15)
u(x, y, t) = σo · F1 (x, t) · F2 (y, t)
(16)
W celu zilustrowania wyników obliczeń przy wykorzystaniu wyprowadzonych
wzorów od (10) do (16) przedstawiono wykresy zanikania ciśnienia porowego na rys. 3
4
Obliczenia przeprowadzono dla hipotetycznego obszaru przeciążonego o wymiarach: B = 80
m, L = 120 m, H = 8m, oraz następujących parametrach Me = 300 kPa , kx=ky=10-6 m/s;
1 dzień
1 rok
2 lata
Rys. 3 Wyniki obliczeń osiadania warstwy konsolidowanej w czasie oraz wyniki obliczeń
zanikania ciśnienia w porach (L=120m; B=80 m; Me=300 kPa; kx=ky=10-6 m/s [5]
1 dzień
5
1 rok
2 lata
Rys. 4 Wyniki obliczeń osiadania warstwy gruntu stałego oraz zmian ciśnienia w porach
zmiennych w czasie (L= 40 m; B=250 m; ko=10-6 m/s; Meo= 300 kPa; κ1= 1,75; no= 0,23), [5]
Na rys. 4 przedstawiono wyniki obliczeń osiadania docelowego przy założeniu, że
parametry gruntowe: współczynnik filtracji k oraz edometryczny moduł ściśliwości zmieniają
się w trakcie konsolidacji. Zmiany te przyjęto zgodnie z wcześniejszymi badaniami [1]

s 

Me( s ) = Meo ⋅ 1 −
 no H o 
−κ

s 

k ( s ) = k0 ⋅ 1 −
 no H o 
(17)
− κf
(18)
gdzie: Meo - jest modułem edometrycznym torfu przed przeciążeniem Me( s ) - jest modułem
edometrycznym torfu po uzyskaniu osiadania s w procesie konsolidacji po czasie t, no - jest
porowatością
torfu
przed
przeciążeniem,
Ho -
miąższością
warstwy torfu
przed
przeciążeniem, natomiast odpowiednio ko - jest współczynnikiem filtracji torfu przed
przeciążeniem, k ( s ) - współczynnikiem filtracji torfu po uzyskaniu osiadania s.
6
Wzór (17) pozwala na otrzymanie zależności, która opisuje docelowe osiadanie
warstwy konsolidowanego torfu S∞ (σ o ) po zakończeniu tego procesu [1].
Mamy:
−1


κ


κ − 1 σ o 1 −1 



S∞ (σ o ) = no ⋅ H o ⋅ 1 − 1 +
⋅
 
no Meo  


(19)
Przeprowadzone obliczenia numeryczne, [5] wskazują, że parametry κ oraz κ f zmieniają się
w granicach
1,5 < κ < 2,0
(20)
6,5 < κ f < 8,0
(21)
Powyższe wzory umożliwiają sformułowanie dla rozwiązania ogólnego osiadania i zanikania
ciśnienia porowego w postaci
s (t ) = S ∞ [1 − F1* ( x ,t ) ⋅ F2* ( x ,t )]
 t 
F1* ( x ,t ) = F1  x , * 
 Tox 
 t 
F2* ( y ,t ) = F2  y , * 
 T 
oy 

(22)
oraz
(23)
(24)
Na podstawie wcześniejszych zależności (11) oraz (14) mamy
2
 L' 
γw ⋅ 
2
Tox* =
Me( s ) ⋅ k x (s )
oraz
(25)
2
 B' 
γw ⋅ 
2
Toy* =
Me( s ) ⋅ k y (s )
gdzie
(26)
wielkości Me( s ) oraz k ( s ) opisane są zależnościami (17) i (18). Z zależności (22) ÷ (26)
widać, że rozwiązanie ma postać uwikłaną a osiadanie zależy od zmiany parametrów
gruntowych Me oraz k , które zależą od osiadania. Rozwiązanie otrzymamy metodą
kolejnych iteracji. Analogicznie otrzymamy wzory na zmianę ciśnienia porowego
U ( x , y ,t ) = σ o ⋅ F1* ( x ,t ) ⋅ F2* ( x ,t )
(27)
W równaniu (27) mają zastosowanie zależności od (23) do (26).
7
Przedstawioną metodę można również stosować, gdy obciążenia ściskające torf powodowane
przez warstwę przeciążającą zmieniają się. Może to być spowodowane np. kilkakrotnym
podwyższaniem warstwy popiołów. Mamy wtedy
Rys. 5 Schemat zmian osiadania przy podwyższaniu warstwy przeciążającej wg [3,5,6]
s( t ) = ∑ [s i (t ) ⋅ η (t − t i )]
gdzie
(28)
i =1
0 gdy t < 0
1 gdy t > 0
η (t ) = 
(29)
Si (t ) = S ( x , y ,t ,σ oi )
(30)
Uzyskane zależności analityczne opisujące proces konsolidacji zostały zweryfikowane w
oparciu o badania terenowe.
WERYFIKACJA MODELU MATEMATYCZNEGO
W celu weryfikacji przedstawionego modelu matematycznego konsolidacji torfów
przeciążonych warstwą popiołów przeprowadzono badania eksperymentalne na modelu w
naturze. Konsolidowany obszar położony był na zachodnim brzegu rzeki Odry pomiędzy
Papiernią Skolwin a Hutą Szczecin. Rzędne terenu wahały się pomiędzy 0,4 m i 1,0 m NN.
Wymiary konsolidowanego obszaru w planie to: L = 518 m; B = 268 m. Cały teren stanowiło
torfowisko niskie położone na dolnej terasie rzeki Odry. Torfy miały miąższość od 6 m do 8
m. Pod nimi zalegają osady rzeczne – piaski pylaste.
8
Poziom wody na konsolidowanym obszarze powiązany jest z poziomem wody w rzece
Odrze. Do prac konsolidacyjnych w celu przeciążenia warstwy torfów, wykorzystano popioły
z Elektrowni Dolna Odra. Popioły te o kodzie 10 01 80, nie są zaliczane do odpadów
niebezpiecznych zgodnie z Rozporządzeniem Ministra Środowiska z dnia 27 września 2001
roku w sprawie katalogu odpadów (Dz.U.nr112 poz. 1206). Nasyp przeciążający z popiołów
wykonywano warstwami o grubości ok. 30 cm zagęszczając je. Prace wykonano w latach
2003 – 2005. Po zakończeniu prac związanych z przygotowaniem nadkładu przeprowadzono
badania wód gruntowych oraz wpływu popioło-żużli na naturalne środowisko (florę i faunę).
Nie stwierdzono negatywnego wpływu warstwy przeciążającej na środowisko. Przed
rozpoczęciem prac związanych z konsolidacją torfów przeprowadzono badania geologiczne
podłoża gruntowego. Prace te wykonał Geoprojekt Szczecin. Katedra Geotechniki
Politechniki Szczecińskiej wykonała badania podłoża gruntowego w trzy lata po zakończeniu
budowy nasypu.
Na podstawie tych badań ustalono parametry początkowe do modelu matematycznego
dla warstwy torfów:
- w otworze 22 (przekrój 1) otrzymano
porowatość początkową no = 0 ,80
moduł ściśliwości początkowy M o = 210kPa
współczynnik filtracji początkowy k o = 10 −6 m / s
-
w otworze 34 (przekrój 2) otrzymano
porowatość początkową no = 0 ,80
moduł ściśliwości początkowy M o = 166kPa
współczynnik filtracji początkowy k o = 1,16 ⋅ 10 −5 m / s
Na rys. 6 oraz 7 przedstawiono profil gruntowy w otworze 22 (przekrój 1) oraz profil
gruntowy w otworze 34 (przekrój 2) przed rozpoczęciem konsolidacji, po wykonaniu części
nadkładu po 85 dniach oraz po wykonaniu całego nasypu po 1235 dniach.
1
= 3 7,2 kPa
2
= 69,6 kPa
s 2=1,3 0 m
H 1 =7,02 m
H0 =8,0m
s 1=0, 98 m
4,50 m
16-09- 2004
85 dni
h2 =5,8 0m
2, 12 m
H 2 =6,70 m
=0
h1 =3,1 m
Otwór nr 22
10-1 2-2004
03-02-2008
1235 dni
Rys. 6 Warunki geotechniczne w profilu 1 (otwór 22), wg [5]
9
2 ,81 m
1
= 48,0 kP a
2
= 7 0,8 kPa
s 2=2,3 0 m
16-09-2004
85 dni
H2 =6,30m
H1 =7,31m
H0 =8, 6m
s 1=1 ,29 m
3, 60 m
h 2 =5,90 m
=0
h1 =4,10 m
Otwór nr 34
10- 12-200 4
03-0 2-2008
1235 dni
Rys. 7 Warunki geotechniczne w profilu 2 (otwór 34) wg [5]
Badania gruntowe torfów wykonane w Katedrze Geotechniki Politechniki Szczecińskiej
pozwoliły na przeprowadzenie aproksymacji statystycznej współczynników κ oraz κ f
występujących w równaniach (17) oraz (18). Otrzymano
κ = 1,86 ;
κ f = 7,5
Rozmieszczenia profilów obliczeniowych przedstawiono na rys. 8
Rys. 8 Rozmieszczenie obliczeniowych profili na konsolidowanym obszarze wg. [5]
Obliczenia numeryczne przeprowadzono wykorzystując zależności od (10) do (30)
uwzględniając zmianę parametrów gruntowych w czasie konsolidacji oraz zmianę obciążenia
w trakcie wykonywania nasypu. Przykładowe wyniki obliczeń przedstawiono na rys.9, rys. 10
i rys.11.
10
Rys. 9 Wykres osiadania obszaru konsolidowanego torfu dla x = 0
po 85 dniach i 1235 dniach, przekrój I, wg. [5]
Rys. 10 Wykres osiadania torfu w przekroju II, wg. [5]
Rys. 11 Wykres osiadania torfu w przekroju III, wg. [5]
11
W trakcie prowadzenia konsolidacji przeprowadzono pomiary geodezyjne osiadania
torfu w wybranych miejscach w mniejszych odstępach czasowych. Przykładowo na rys. 12
oraz na rys. 13 pokazano przebieg osiadania w punktach 22 oraz 34 (rys. 8)
Rys. 12 Przebieg osiadania w punkcie 22 wg. [5]
Rys. 13 Przebieg osiadania w punkcie 34 wg. [5]
Na rys. 12 oraz rys. 13 linią przerywaną zaznaczono przebieg osiadania, który
wystąpiłby, gdyby nie było zmiany obciążenia.
12
WNIOSKI
1. W pracy przedstawiono model konsolidacji torfów przeciążonych warstwą popiołów.
Badania objęły sformułowanie modelu matematycznego oraz weryfikację tego modelu
w oparciu o badanie eksperymentalne w naturze.
2. W porównaniu do klasycznego modelu konsolidacji opracowanego przez Terzaghi
model prezentowany w niniejszym opracowaniu różni się:
- przyjęciem warstwy przeciążającej z popiołów, która nie odbiera nadwyżki wody
w procesie konsolidacji, oraz
- przyjęciem zmiennym w czasie konsolidacji parametrów gruntowych: moduł
ściśliwości torfu oraz współczynnik filtracji.
Tak przyjęte warunki konsolidacji powodują, że odpływ filtracyjny wody gruntowej w
procesie konsolidacji odbywa się poziomo. W przypadku modelu Terzaghi przepływ
filtracyjny jest pionowy.
3. Cechą charakterystyczną modelu konsolidacji torfu z filtracją poziomą jest przebieg
osiadania obszaru konsolidowanego, który rozpoczyna się od brzegu tego obszaru i
tam przebiega najszybciej. Najwolniej osiada część środkowa obszaru
konsolidowanego. Tam najwolniej zanika nadwyżka ciśnienia porowego.
4. Badanie eksperymentalne na obiekcie w naturze potwierdziły sposób przebiegu
osiadania warstwy torfów w warunkach, kiedy odpływ filtracyjny odbywa się w
kierunku poziomym, w szczególności badania potwierdziły wnioski z części
analitycznej pracy, że
- uwzględnienie w opisie matematycznym procesu konsolidacji, modułu ściśliwości
torfu zmiennego w czasie pozwala dokładniej prognozować osiadanie docelowe,
oraz
- uwzględnienie w obliczeniach współczynnika filtracji torfu zmiennego w czasie
wpływa na wydłużanie czasu konsolidacji i lepiej przybliża czas rzeczywisty.
5. Badania eksperymentalne potwierdziły fakt iż z dokładnością wystarczającą dla
celów inżynierskich zastosowany model może być wykorzystany w projektowaniu
wzmacniania podłoża gruntowego zbudowanego z torfów.
Literatura
1. Meyer Z.: Empirical Model at Peat Consolidation, International Conference
Advances in Understanding and Modeling of Mechanical Behavior of Peat. Delft
1993.
2. Meyer Z., Dereczennik M.: Effect of Consolidation on Compressibility Modulus in
Organic Soil, Prace Naukowe Politechniki Szczecińskiej, Geotechnika VIII. Szczecin
1992.
3. Meyer Z., Szczygielski T., Bednarek R.: Metoda obliczania osiadania gruntu
organicznego obciążonego popioło-żużlami, Międzynarodowa Konferencja
EUROCOALASH - Warszawa, 2008.
4. Meyer Z., Szczygielski T., Bednarek R.: Popiół z węgla w inżynierii geotechnicznej –
uzdatnianie gruntów słabych, Międzynarodowa Konferencja EUROCOALASH Warszawa 2008
13
5. Szczygielski T.: Praca doktorska pt. Analiza warunków konsolidacji torfów
przeciążonych warstwą popiołów, obroniona na WBiA ZUT, Szczecin 2009.
6. Szczygielski T., Meyer Z.: Analiza warunków konsolidacji torfów przeciążonych
warstwą popiołów, 55 Konferencja Naukowa KILiW PAN, Krynica 2009.
7. Szymański A., Sas W.: Parametry geotechniczne w opisie procesu konsolidacji
gruntów organicznych, Sesja Naukowa Geotechnika w Budownictwie i Inżynierii
Środowiska poświęcona 47 leciu Pracy Naukowej i 70 leciu urodzin prof. E.
Dembickiego, Politechnika Gdańska. Gdańsk 2000.
8. Wiłun Z.: Zarys Geotechniki, Wyd. Kom. i Łączności. Warszawa 1992.
Streszczenie
W pracy przedstawiono analizę konsolidacji torfów przeciążonych popiołami. Popioły z uwagi na
bardzo mały współczynnik filtracji uniemożliwiają odprowadzenie nadwyżki wody gruntowej w
kierunku pionowym i z tego powodu filtracja wody uniemożliwiająca konsolidację odbywa się w
kierunku poziomym. Model konsolidacji uwzględnia zmianę parametrów torfu : modułu ściśliwości
oraz współczynnika filtracji w trakcie konsolidacji stosownie do zmian porowatości gruntu.
Przedstawiono również wyniki weryfikacji tego modelu w oparciu o badania terenowe
14