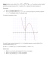9. równania różniczkowe cząstkowe

9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
1

9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
Wstęp.
Równania zawierające pochodną nieznanej funkcji dwóch lub więcej zmiennych nazywa się
cząstkowym równaniem różniczkowym. Na przykład:
 2u
 2u
 2 xy
u 1
x2
y 2
3u
 2u
x
 8u  5 y
x2 y
y 2
(9.1)
3
3
  2u 

 6  u  x
 x2 
 xy 2


 2u
u
 xu
x
2
y
x
Ze względu na szerokie zastosowanie w mechanice konstrukcji, nasze rozważania ograniczą się do
równań różniczkowych cząstkowych liniowych drugiego rzędu (rząd określa maksymalną pochodną jaka
występuje w równaniu) z dwiema zmiennymi. Dla takich równań można zapisać postać kanoniczną jako:
A
 2u
 2u
 2u

B

C
 D0
xy
x 2
y 2
(9.2)
RRC liniowe drugiego rzędu można sklasyfikować jako:
Wyznacznik
B 2  4 AC
RRC
<0
Eliptyczne
=0
Paraboliczne
>0
Hiperboliczne
Przykład
Równanie Laplace’a
(równanie opisuje stan ustalony,
brak zmiennej czasowej)
 2T  2T

0
x 2 y 2
Zagadnienie propagacji
rozkład funkcji w czasie i przestrzeni
(równanie przewodnictwa cieplnego)
T
 2T
k 2
t
x
Równania falowe
rozkład funkcji w czasie i przestrzeni
(rozwiązania oscylacyjne np. drgania struny)
 2T 1  2T

 t 2 c x 2
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
2

9.1 Równania różniczkowe cząstkowe eliptyczne.
ciepło
zimno
Zapora wodna
Linia przepływu
Linie ekwipotencjalne
zimno
przewodnik
Warstwa
nieprzepuszczalna
a)
b)
c)
Rys.9.1 Przykłady RRC eliptycznych.
a) rozkład temperatur na podgrzewanej płycie,
b)stan ustalony przepływu wody pod tamą c) rozkład pola elektrycznego w okolicy izolatora.
Równanie Laplace’a jest typowym przykładem równania różniczkowego cząstkowego eliptycznego:
 2T  2T

0
x 2 y 2
(9.3)
Gdy prawa strona nie jest równa zeru, to mamy równanie rrc Poissona.
 2 T  2T

 f ( x, y)
x 2 y 2
(9.4)
Korzystając z metody różnic skończonych równanie różniczkowe Laplace`a można sprowadzić do
algebraicznego układu równań. Pochodne cząstkowe zastępujemy odpowiednimi różnicami skończonymi:
 2 T Ti 1 , j  2Ti, j  Ti1 , j

x 2
x2
 2 T Ti , j 1  2Ti, j  Ti, j 1

y 2
y 2
(9.5)
Równania (9.5) podstawiamy do równanie (9.3) co w rezultacie daje:
Ti 1, j  2Ti , j  Ti 1, j
x
2

Ti, j 1  2Ti , j  Ti , j 1
y 2
0
(9.6)
Dla siatki kwadratowej (rys9.2) równanie (9.6) przyjmuje postać:
Ti 1, j  Ti 1, j  Ti , j 1  Ti , j 1  4Ti , j  0
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.7)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
3

y
0, n+1
i,j+1
i,j
i-1,j
i+1,j
i,j-1
0,0
m+1, 0
x
Rys.9.2 Siatka metody różnic skończonych.
Aby znaleźć rozwiązanie zadania musimy zdefiniować warunki brzegowe tzw. warunki brzegowe Dirichleta.
Przykład 9.1:
W zadaniu określone są warunki brzegowe. Należy obliczyć temperatury w określonych miejscach płyty.
100˚ C
4
3
2
75˚ C
1,3 2,3
3,3
2,2
3,2
1,2
50˚ C
1
1,1
0
3,1
2,1
1
2
0˚ C
3
4
Rys.9.3 Płytka podgrzewana różnymi temperaturami z różnych stron.
Obliczenia wykonujemy korzystając ze wzoru (9.7).Dla punktu (i,j) = (1,1) mamy:
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
4

T2,1  T0,1  T1, 0  T1, 2  4T1,1  0
(9.8 a)
Do równania (9.8 a) podstawiamy warunki brzegowe i otrzymujemy:
T2,1  75  0  T1, 2  4T1,1  0
T2,1  T1, 2  4T1,1  75
(9.8 b)
Podobną procedurę należy przeprowadzić dla pozostałych punktów, a następnie rozwiązać powstały układ
równań. Ostatecznie otrzymujemy rozwiązanie:
T1, 3  78 ,58718 T2, 3  76 ,06402 T3,3  69,71050
T1, 2  63,21152 T2, 2  56,11238 T3, 2  52,33999
T1,1  43,00061 T2,1  33,29755 T3,1  33,88506
Znając rozkład temperatury, możemy również obliczyć pochodne temperatury względem x i y obrazujące
tak zwany strumień ciepła. Zależność tę opisują równania Fouriera:
T Ti 1  Ti1

  kx q x
x
2 x
T T j 1  T j 1

 k y q y
y
2 y
(9.9)
Gradient temperatury w punkcie obliczamy ze wzoru:
ar ctg
qn 
qy
qx
q x2

(9.10)

q 2y
Rozpatrzmy teraz przypadek, gdy warunki brzegowe wyrażone są przez pochodne temperatury, czyli
strumienie ciepła. Są to tzw. Warunki brzegowe Neumann`a.
Rys.9.4.Warunki brzegowe Neumann`a (dla i=0)
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
5

Równanie różnicowe zapisane dla punktu (0,j) ma postać:
T1, j  T1, j  T0, j 1  T0, j 1  4T0, j  0
(9.11)
Należy zwrócić uwagę na punkt (-1,j), który mimo że leży poza obszarem jest również wymagany w
równaniu. Wydawać by się mogło, że punkt ten będzie stanowił problem, ale tu właśnie przychodzi z
pomocą warunek brzegowy w postaci pochodnej. Należy określić pierwszą pochodną po zmiennej x w
punkcie (0,j):
T T1, j  T1, j

x
2 x 2
T1 , j  T1, j
T
 2 x
x
(9.12)
Teraz mając zależność (9.12) możemy podstawić ją do wzoru (9.11):
2T1, j  2x
T
 T0 , j 1  T0, j 1  4T0 , j  0
x i
(9.13)
Warunki brzegowe dla nieregularnych kształtów.
Rozpatrzmy obraz nieregularnego brzegu jak na Rys.9.5.
α1Δx
β2Δy
α2Δx
β1Δy
i,j
Rys.9.5. Obraz nieregularnego brzegu.
Korzystając z różnicy centralnej w tył otrzymujemy:
Ti , j  Ti 1, j
 T 

 
1 x
 x i 1, i
Ti1, j  Ti, j
 T 

 
 2 x
 x  i,i 1
Obliczając drugą pochodną wyrażenia (9.14) względem zmiennej x, mamy:
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.14)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
6

 T 
 T 
 
 
 T   T   x i , i 1  x  i 1, i
  

 1 x   2 x
x 2  x  x 
2
Ti 1 , j  Ti , j Ti , j  Ti 1 , j

 2 x
1 x


 1 x   2 x
2
 Ti 1, j  Ti , j 
2  Ti 1, j  Ti , j
 2 


x  2 (1   2 ) 1 (1   2 ) 
Ti 1, j  Ti , j 
2  Ti 1, j  Ti , j
 2 


x 1 (1   2 )  2 ( 1   2 ) 
2
(9.15)
Wyrażenie na pochodną względem zmiennej y wygląda analogicznie:
2 T
2

2
y
y 2
Ti 1, j  Ti , j 
 Ti 1 , j  Ti , j



 1 ( 1   2 )  2 (  1   2 ) 
(9.16)
Określenie T przy nieregularnych kształtach:
x
Rozpatrzmy ponownie obszar o nieregularnym kształcie i zapiszmy rozwiązanie w punkcie 3:
y
2
3
8
η
1
4
7
Δy
5
6
Δx
Rys. 9.6. Brzeg zakrzywiony.
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
x
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
7

x
T8
T6
T7
78
76
Rys. 9.7. Liniowa zależność między T8 , T7 , T6
Zakładamy, że T1 , T3 , T7 i T8 , T7 , T6 zmieniają się liniowo.Pochodna w punkcie 3 ma postać:
T  T7
T
 1
 3
L17
T1
T
T

 7
L17  3 L17
T1 
(9.17)
T
 L17  T7
 3
cos 
x
L17
(9.18)
Z proporcji można zapisać (rys. 9.7.):
x
T T
L
 6 8 tg   78
L78
y
x
T  T   x  tg
x 6 8
y
x  tg 
T7  T8  T6  T8 
y
(9.19)
Podstawiając do wzoru (9.17) wzory (9.18) i (9.19) otrzymujemy:
T1 
T
x
x  tg 

 T8  T6  T8 

  3 cos
y
 x  tg  
T
x
x  tg 


 T6
 T8 1 

  3 cos
y
y 

Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.20)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
8

9.2. Równania różniczkowe cząstkowe paraboliczne.
RRC paraboliczne umożliwiają znalezienie rozkładu zmiennej w funkcji czasu. Przykładem może
być równanie opisujące przewodnictwo cieplne w postaci:
kx
 2T
2T
 2T T

k

k

y
z
t
x 2
y 2
z 2
(9.21)
ciepło
t=3Δt
t=2Δt
t=Δt
zimno
t=0
zimno
ciepło
T
x
a)
b)
Rys. 9.8 Zastosowanie RRC parabolicznego.
a)obraz długiego pręta izolowanego podgrzewanego z jednej strony,
b) Rozwiązanie zagadnienia stanów podgrzewanego pręta w różnych chwilach w czasie.
Przy założeniu, że ciało jest izotropowe k x  k y  k z oraz przepływ ciepła następuje tylko po jednym
kierunku, równanie przewodnictwa cieplnego ma postać:
T
 2T
 k 2 gdzie k – to stała przewodzenia
t
x
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.22)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
9

l
0, n+1
i,l+1
i,j
i-1,j
i+1,j
i,j-1
0,0
1
2
3
m
Rys.9.9. Dyskretyzacja przestrzenna (m) i czasowa (l)
Metody typu „explicit” (jawne).
Równania przewodnictwa ciepła wymagają aproksymacji drugiej pochodnej przestrzeni i pierwszej
pochodnej czasu. Równania te są reprezentowane podobnie jak równania Laplace’a metodą różnic
skończonych centralnych:
 2 T Ti l1  2Ti l  Til1

x 2
x 2
(9.23)
Aby określić przestrzeń czasową wykorzystujemy schemat różnicowy w przód:
T Til 1  Til

t
t
(9.24)
Podstawiamy równania (9.23) i (9.25) do wzoru (9.22) i otrzymujemy:
k
Ti l1  2Ti l  Ti l1 Til 1  Til

t
x2
(9.25)
Po przekształceniach otrzymujemy równanie dla wszystkich punktów wewnętrznych:

Ti l 1  Ti l   Ti l1  2Ti l  Ti l1

, gdzie  
kt
x 2
Widać, że do wyznaczenie rozwiązania w danym kroku wykorzystujemy wartość obliczoną w kroku
poprzednim.
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.26)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
10

l+1
l
i-1
i+1
i
Rys. 9.10. Komórka obliczeniowa
zimno
ciepło
Przykład 9.2:
Wykorzystanie metody „explicit” do obliczenia rozkładu temperatury dla długiego izolowanego pręta (patrz
rys. 9.11.):
Rys. 9.11. Pręt dany w zadaniu
Dane:
Długość =10cm
x  2cm
t  0,1s
dla t  0
T (0)  T0( 0 )  100 C
0
T (10 )  T5( 0 )  50C
0,835  (0,1)
 0,020875
22
T1( 0)  T2( 0)  T3( 0)  T4( 0 )  0
2
3
4
5
l=10 cm
k  835 ,0 cm2 / s

1
Rys. 9.12 Podział pręta na jednakowe odcinki
Wykorzystując zależność (9.26) możemy zapisać dla t  0,1s x  2,4,6,8 :
T11  0  0,020875 [0  2 (2,0875 )  100 ]  2,0875
T21  0  0,0020875 [0  2(0)  0]  0
T31  0  0,020875 [0  2 (0)  0]  0
T41  0  0,020875 [50  2 (0)  0]  1,0438
Dla t  0,2s x  2,4,6,8 wygląda to następująco:
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
11

T121  2,0875  0 ,020875 [0  2( 2,0875 )  100 ]  2,0875
T22  0  0,020875 [0  2(0 )  2 ,0875 ]  0,043577
T32  0  0,020875 [1,0438  2( 0)  0 ]  0,021788
T42  1,0438  0,020875 [50  2 (1,0438 )  0]  2,0439
Dla kolejnych t obliczenia wykonujemy analogicznie.
Na Rys.9.13 przedstawiono graficznie rozwiązanie równania dla chwil t  3, 6, 9,12
T
t=3
80
Δx=2
Δt=0,1 [s]
k=0,835
t=12
t=9
t=6
40
2
4
6
8
10
x
Rys. 9.13. Rozkład temperatury dla różnych chwil czasu.
Problem zbieżności i stabilności to:
Metoda całkowania jest zbieżna gdy, dla:
x  0
t  0
(9.27)
otrzymujemy rozwiązanie dokładne. Metoda jest stabilna gdy błędy nie narastają podczas całkowania
problemu. Stabilność można uzyskać narzucając ograniczenia na krok czasowy. Można wykazać, że gdy:
1
lub
2
1 x 2
t  
2 k

(9.28)
Metda całkowania "explicit" jest stabilna.
1
błędy nie narastają, ale mogą oscylować
2
1
gdy  
nie ma oscylacji
4
1
a gdy  
otrzymujemy minimalny błąd metody
6
Gdy  
Brak stabilności w przykładzie obrazuje poniższy wykres, który sporządzono   0,735 .
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.29)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
12

T
T
t =6
100
T
t =12
100
100
x
T
x
T
t =24
100
t =18
t = 30
100
x
x
Rys. 9.14. Brak stabilności przy zbyt dużym λ
Metody typu „implicit” (niejawne)
Z powyższych rozważań wynika, że metoda „explicit” może prowadzić do dużych błędów przy
nieograniczonym kroku całkowania. Konieczne są więc restrykcyjne ograniczenia, aby zachować stabilność.
Metody „implicit” są pozbawione tego mankamentu kosztem bardziej skomplikowanych algorytmów.
Fundamentalna różnica pomiędzy metodami „explicit” a „implicit” jest pokazana na rys.9.15.:
l+1
l+1
l
i-1
i
i+1
l
i-1
i
i+1
Rys 9.15. Różnica omawianych metod Po lewej "explicit", po prawej "implicit".
W przypadku metody „implicit” pochodną określa się w czasie l+1 :
 2 T Ti l11  2  Ti l 1  Ti l11

x2
x2
(9.30)
Aby określić przestrzeń czasową wykorzystujemy schemat różnicowy w przód:
T Ti l 1  Ti 1

x
t
Wykorzystując podstawowy wzór na równanie paraboliczne (9.20) otrzymamy:
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.31)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
13

k
Ti l11  2  Til 1  Ti l11 Til 1  Til

t
x 2
(9.32)
Równanie to można uprościć do postaci:
 Ti l11  (1  2 )Ti l 1  Ti l11  Ti l
gdzie

kt
(x) 2
(9.33)
Dla układów, gdy dane są temperatury określone na brzegach, mamy:
T0l 1  f 0 (t l 1 )
(9.34)
gdzie f 0 (t l 1 ) jest funkcją określającą jak temperatury na brzegach zmieniają się w czasie.
Dla pierwszego punktu wewnętrznego i = 1 mamy :
(1  2 )T1l 1  T2l 1  T1l    f 0 (t l1 )
(9.35)
a dla ostatniego punktu wewnętrznego i = m mamy równanie:
 Tml 11  (1  2 )Tml 1  Tml    f m (t l 1 )
Ciąg dalszy przykładu 9.2.
Równanie dla   0,020875 t  0 i  1 :
1,04175  T11  0,020875  T21  0  0,020875  100 
Analogicznie dla pozostałych punktów zapisujemy równania i otrzymujemy układ równań w postaci:
 0,020875
0
 1,04175
 0,020875
1,04175
 0,020875


0
0,020875  0,020875

0
0
 0,020875

0
 T11   2,0875 
  1  0 
0
  T2   

 0,020875  T31   0 
   

1,04175  T41  1,04385 
Otrzymujemy rozwiązanie dla chwili t=0:
T11  2,0047
T21  0,0406
T31  0,0209
T41  1,0023
Dla kolejnej chwili t = 1 otrzymujemy nowy układ równań, któy należy ponownie rozwiązać.
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.36)
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
14

Metoda Cranka - Nicolsona
Jest to ulepszenie metody implict, które polega na zwiększeniu dokładności całkowania w czasie.
Metoda ta nie wymaga dodatkowych ograniczeń ze względu na czas i przestrzeń. Jest to możliwe dzięki
zastosowaniu metody punktu środkowego (obliczenie pochodnej centralnej w 2 punktach co daje znacznie
większą precyzję).
l+1
l+1/
l2
i-1
i
i+1
Rys. 16. Graficzna interpretacja metody Cranka -Nicolsona
l 1
1
T Ti  Ti

x
t
dla
t
l
1
(9.37)
2
Druga pochodna w przestrzeni jest określana w punkcie pośrednim, co powoduje uśrednienie przybliżeń w
początku t l i końcu t l 1 i w rezultacie daje dużo większą dokładność:
 
 
 2 T 1  Ti l1  2Ti l  Ti l1 Ti l11  2  Ti l 1  Ti l11 
 


x2 2 
x 2
x2

(9.38)
Ciąg dalszy przykładu 9.2.:
Analitycznym rozwiązaniem RRC parabolicznego
T
 2T
 k 2 jest:
t
x
2 2
x  2


T T   
 1n sin nx  exp  n 2 kt 
l
 l 


 l n 0 n
Porównanie wyników metod: „explicit” , „implicit” i Cranka - Nicolsona (przykład 9.2.)
∆t
10
5
2
1
0,5
0,5
λ
2,0875
1,04375
0,4175
0,20875
0,104375
0,04175
explicit
208,75
-9,13
67,12
65,91
65,33
64,97
implicit
53,01
58,49
62,22
63,49
64,12
64,49
Crank - Nicolson
79,77
64,79
64,87
64,77
64,74
64,73
Rozwiązanie dokładne T x  2, t  10  64,8018C
Jak widać metoda C - N jest najdokładniejsza od samego początku, a metoda explicit dała
satysfakcjonujący wynik dopiero wtedy, gdy współczynnik λ spełnił założenia ograniczenia co do wielkości
kroku całkowania.
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
9. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
15

9.3. Równania różniczkowe cząstkowe hiperboliczne.
Rozpatrzmy równanie drgań struny:
2
2w
2  w

c
t 2
x 2
E
gdzie c 

E – moduł Young’a
 - gęstość ośrodka
c - prędkość
(9.39)
i+1
Δt
i
Δt
i-1
Δt
i-1
Δx
i
i+1
Δx
Rys. 9.17 Siatka wykorzystana w zadaniu
Wykorzystując metodę różnic skończonych możemy zapisać:
l
l
l
 2 w wi 1  2 wi  wi 1

x 2
x2
 2 w wil 1  2 wli  wil 1

t 2
t 2
(9.40)
Podstawiając równania (9.40) do wzoru (9.39) otrzymujemy:
c2 
wil1  2 wil  wil1
x2

wil 1  2 wli  wil 1
t 2
(9.41)
Po przekształceniach mamy:


wil 1   2 wil1  2 1   2 wil   2 wil1  wil 1
(9.42)
c  t
gdzie  
x
Równanie (9.42) jest typu explicit. Można wykazać, że rozwiązanie to jest stabilne, gdy   1 oraz jest
najdokładniejsze dla   1 . Wtedy nasze równanie przyjmuje postać:
wil 1  wil1  wil1  wil 1
Metody Komputerowe – Dominika Mejbaum, Anna Snela, Marek Komosa
(9.43)