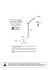Zasada zachowania energii - Open AGH e

Zasada zachowania energii
Autorzy: Zbigniew Kąkol, Kamil Kutorasiński
Pokazaliśmy, że gdy na ciało działa tylko siła zachowawcza, to dla dowolnej drogi z A do B
W = ΔEk = EkB − EkA
(1)
W = −ΔEp = −(EpB − EpA )
(2)
−(EpB − EpA ) = EkB − EkA
(3)
EkA + EpA = EkB + EpB .
(4)
skąd wynika, że
lub
Równanie ( 4 ) wyraża zasadę zachowania energii mechanicznej.
PRAWO
Prawo 1: Zasada zachowania energii mechanicznej
Zasada zachowania energii mechanicznej mówi, że dla ciała podlegającego działaniu siły zachowawczej, suma energii
kinetycznej i potencjalnej jest stała.
Podaliśmy zasadę zachowania energii mechanicznej dla pojedynczego ciała, ale ta zasada jest bardziej ogólna i obowiązuje dla
wszystkich odosobnionych układów ciał. Układy odosobnione to takie, na które nie działają siły zewnętrzne (spoza układu). W
takich układach suma energii kinetycznych i potencjalnych wszystkich ciał pozostaje stała bez względu na oddziaływania w nich
zachodzące.
PRZYKŁAD
Przykład 1: Skoczek na linie
Skoczek na linie "bungee" skacze z punktu A i osiąga najniższy punkt B tak jak na Rys. 1. Skoczek korzysta z liny o długości l,
która rozciąga się sprężyście ( F = −kx), aż do zerwania, co następuje gdy lina wydłuży się o x = 50% w stosunku do
długości początkowej. Ile razy wytrzymałość liny na zerwanie musi być większa niż ciężar skoczka,żeby lina nie urwała się?
Rysunek 1:
W punkcie A grawitacyjna energia potencjalna skoczka liczona względem powierzchni Ziemi wynosi mgh (masę liny
pomijamy), natomiast energia potencjalna sprężystości liny równa się zeru, bo lina nie jest rozciągnięta. Całkowita energia
mechaniczna układu w punkcie A wynosi więc
EA = mgh.
(5)
Natomiast energia całkowita układu w punkcie B
EB = mg(h − l − x) +
kx2
2
(6)
jest sumą grawitacyjnej energii potencjalnej skoczka i energii potencjalnej sprężystości rozciągniętej liny równanie Energia
potencjalna-( 9 ).
Ponieważ siły grawitacji i sprężystości są siłami zachowawczymi więc energia mechaniczna jest zachowana. Uwzględniając,
że energia kinetyczna skoczka w punktach A i B jest równa zeru otrzymujemy
mgh = mg(h − l − x) +
kx2
2
(7)
lub
kx2
2
− mgl − mgx = 0.
(8)
Wstawiając do tego równania maksymalne możliwe wydłużenie liny x = 0.5 możemy obliczyć graniczny współczynnik k liny
k=
12mg
,
l
(9)
skąd otrzymujemy
F = kx =
12mg l
2
l
= 6mg.
(10)
Wytrzymałość liny na zerwanie musi być co najmniej 6 razy większa niż ciężar skoczka.
Teraz spróbujemy odpowiedzieć na pytanie czy energia jest zachowana w przypadku, gdy w układzie działa siła niezachowawcza.
Jeżeli oprócz siły zachowawczej Fz działa jeszcze siła niezachowawcza Fnz (np. tarcie), to z twierdzenia o pracy i energii
otrzymujemy
Wz + Wnz = ΔEk ,
(11)
Wnz = ΔEk + ΔEp .
(12)
a ponieważ Wz = − ΔE p , to
Widzimy, że siła tarcia zmienia energię mechaniczną układu (zmniejsza ją bo tarcie jest siłą rozpraszającą). Pozostaje wyjaśnić co
stało się ze "straconą" energią mechaniczną. Okazuje się, że zostaje ona przekształcona na energię wewnętrzną U , która objawia
się wzrostem temperatury ciała i otoczenia. Zmiana energii wewnętrznej ΔU jest równa rozproszonej energii mechanicznej
ΔEk + ΔEp + ΔU = 0.
Z równania ( 13 ) wynika, że
PRAWO
(13)
Prawo 2: Zasada zachowania energii
Energia całkowita, tj. suma energii kinetycznej, energii potencjalnej i energii wewnętrznej w układzie odosobnionym nie
zmienia się. Mamy więc zasadę zachowania energii całkowitej. Inaczej mówiąc energia może być przekształcana z jednej
formy w inną, ale nie może być wytwarzana ani niszczona; energia całkowita jest wielkością stałą.
Na zakończenie uwzględnijmy jeszcze dodatkowo siłę Fzew wywieraną na układ przez czynnik zewnętrzny. Jeżeli działa taka siła
to równanie ( 11 ) przyjmuje postać
Wzew + Wz + Wnz = ΔEk
(14)
Wzew = ΔEk + ΔEp + ΔU.
(15)
i w konsekwencji otrzymujemy
Praca wykonana przez czynnik zewnętrzny równa jest sumie zmian energii kinetycznej, potencjalnej i energii wewnętrznej układu.
W ten sposób uwzględniliśmy już całą energię.
Zasada zachowania energii należy do najbardziej podstawowych praw fizyki. Wszystkie nasze doświadczenia pokazują, że jest to
prawo bezwzględnie obowiązujące; nie znamy wyjątków od tego prawa.
ZADANIE
Zadanie 1: Odbicia piłki
Treść zadania:
Piłkę puszczono swobodnie z pewnej wysokości h nad podłożem. Podczas odbicia piłka traci 1/3 swojej energii
mechanicznej, która zamienia się na energię wewnętrzną. Oblicz na jaką wysokość wzniesie się piłka po 4-tym odbiciu i ile
energii mechanicznej zamieniło się w energię wewnętrzną? Wynik zapisz poniżej.
Wskazówka: Skorzystaj z zasady zachowania energii całkowitej.
h4 =
ROZWIĄZANIE:
Dane: h , strata energii mechanicznej przy odbiciu od podłoża s = 1/3
Piłka puszczona z wysokości h nad podłożem posiada energię potencjalną Ep = mgh (względem podłoża). W trakcie
spadania energia potencjalna zamienia się całkowicie w energię kinetyczną. W chwili odbicia s = 1/3 z energii kinetycznej
jest zamieniana na energię wewnętrzną, więc po odbiciu energia kinetyczna (mechaniczna) jest równa q = 1 − s = 2/3
energii przed odbiciem.
Oznacza to, że energia potencjalna jaką uzyska ciało przy wznoszeniu będzie równa 2/3 energii początkowej, a tym samym
ciało po odbiciu wzniesie się na 2/3 wysokości początkowej. Możemy więc napisać ogólne wyrażenie na wysokość po n-tym
odbiciu od podłoża
hn = qhn−1 ,
h0 = h
(16)
gdzie n = 1, 2, 3, . . . . Zgodnie z tym oznaczeniem h 0 = h jest początkową wysokością z jakiej spada ciało. Widzimy, że
kolejne wysokości tworzą ciąg geometryczny. Stąd
4
h4 = hq 4 = h( 23 ) =
16
81
h.
(17)
Analogicznie energia mechaniczna zamieniona na energię wewnętrzną (podczas 4-ech odbić) wynosi
ΔE = mgh − mgh4 =
65
81
mgh
(18)
Jak widzieliśmy na przykładzie omawianym w ćwiczeniu powyżej, w zderzeniach nie musi być zachowana energia mechaniczna.
Okazuje się jednak, że w zderzeniach spełniona jest też inna zasada zachowania; Zasada zachowania pędu.
http://epodreczniki.open.agh.edu.pl/openagh-simulation.php?fileId=1077
http://epodreczniki.open.agh.edu.pl/openagh-simulation.php?fileId=1079
Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne
prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod
warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko
na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie
http://creativecommons.org/licenses/by-sa/3.0/pl/.
Czas generacji dokumentu: 2015-07-10 13:26:40
Oryginalny dokument dostępny pod adresem: http://epodreczniki.open.agh.edu.pl/openagh-permalink.php?
link=5473e02930f40bd95de0bd3f707b0445
Autor: Zbigniew Kąkol, Kamil Kutorasiński