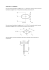1.14. Zginanie poprzeczne

1.14. ZGINANIE POPRZECZNE
1.14.1. Wprowadzenie
Zginanie poprzeczne (zginanie ze ścinaniem) występuje wtedy, gdy obciążenie
zewnętrzne pręta redukuje się do momentu zginającego M y i siły poprzecznej Tz .
W przekroju takim występują naprężenia normalne σ x , wywołane momentem zginającym
M y , oraz naprężenia styczne (ścinające) τ xz i τ xy , wywołane siłą poprzeczną Tz (rys. 1).
Rys. 1
Zatem w przypadku zginania ze ścinaniem macierz naprężeń ma następującą postać:
σ x τ xy
[σ ij ] = τ yx 0
τ zx 0
przy czym naprężenia τ xy
cienkościennych.
τ xz 
0
0



(1)
odgrywają istotna rolę tylko w przypadku przekrojów
Na powierzchni bocznej (pobocznicy) pręta, o wektorze normalnym n(0, ny , nz ) , mamy
p̂(0,0, p̂z ) na części obciążonej i p̂(0,0,0 ) – na nieobciążonej, gdzie pˆ z = −q jest zadanym
obciążeniem (rys. 2). Ponieważ na pobocznicy pręta mamy pˆ x = 0 oraz nx = 0 , zatem z
warunku brzegowego (1.6.7’)1 wynika, iż w punktach leżących na tej powierzchni
px = σ x nx + τ xy ny + τ xz nz = τ xy ny + τ xz nz = pˆ x = 0
(2)
Jeśli przyjąć, że naprężenia styczne w przekroju poprzecznym pręta są współrzędnymi
wektora τ x (0,τ xy ,τ xz ) , to na konturze przekroju poprzecznego mamy
τ x ⋅ n = τ xy ny + τ xz nz
Podstawiając (2) do (3) dostajemy
(3)
τx ⋅ n = 0
(4)
Z powyższego warunku wynika, że wektor τ x jest styczny do konturu przekroju
poprzecznego pręta (rys. 2).
Rys. 2
Wywołane przez siłę poprzeczną naprężenia styczne powodują deplanację (spaczenie)
przekroju poprzecznego pręta, zatem w przypadku zginania poprzecznego nie jest
spełniona hipoteza płaskich przekrojów. Hipoteza ta była wykorzystana przy
wyprowadzeniu wzoru (1.10.12) określającego rozkład naprężeń normalnych w przekroju
przy prostym zginaniu. Zakładając jednak, że siła poprzeczna nie wpływa na rozkład
naprężeń normalnych w przekroju pręta, możemy wzór ten wykorzystać również do
obliczania naprężeń również przy zginaniu poprzecznym. Należy jednak pamiętać o tym,
że założenie to jest słuszne jedynie w przypadku prętów długich, kiedy to h l << 1, gdzie h
jest wysokością przekroju pręta, zaś l – jego długością.
Zatem w przypadku zginania poprzecznego
σx = −
My
Iy
z
(5)
gdzie I y jest momentem bezwładności względem centralnej osi Oy . Pozostałe naprężenia
normalne, czyli σ y oraz σ z są zaniedbywanie małe w stosunku do σ x .
1.14.2. Wzór ŻURAWSKIEGO
Wyznaczenie naprężeń stycznych τ xz w przypadku pręta o dowolnym kształcie przekroju
poprzecznego jest zagadnieniem trudnym. Ponieważ zarówno przekrój poprzeczny
rozważanego pręta, jak i przyłożone obciążenie zewnętrzne są symetryczne względem osi
Oz , to możemy również przyjąć symetryczny rozkład naprężeń τ xz po szerokości
przekroju względem tej osi (rys. 3).
Znając rozkład naprężeń normalnych σ x w przekroju pręta oraz zastępując rzeczywistą
wartość naprężeń τ xz w punktach leżących na linii równoległej do osi Oy ich wartością
uśrednioną τ xz (rys. 3), a więc przyjmując
τ xz (y , z ) = τ xz (z )
(6)
Rys. 3
możemy uśrednione naprężenia styczne τ xz wyznaczyć z warunku równowagi sił
działających na elementarny wycinek pręta (rys. 4)
Rys. 4
Warunek ten ma postać (pamiętamy, że τ xz = τ zx )
∫ (σ
A∗
x
− σ x − dσ x )dA − τ xz (z )b(z )dx = 0
(7)
gdzie A∗ jest polem powierzchni części przekroju powyżej linii równoległej do osi Oy
przechodzącej przez punkt o współrzędnej z , w którym wyznaczamy naprężenie styczne,
zwanej częścią odciętą przekroju poprzecznego pręta, σ x – naprężeniem normalnym w
punkcie przekroju o współrzędnej z ∗ , τ xz – średnim naprężeniem stycznym
(ścinającym) w punkcie o współrzędnej z , b(z ) – szerokością przekroju b(z ) jest
szerokością przekroju poprzecznego na poziomie punktu z , w którym wyznaczamy
naprężenia styczne.
Przekształcając powyższą zależność otrzymujemy
τ xz = −
1
dσ x dA
b(z )dx ∫A∗
(8)
Ponieważ ze wzoru (5) wynika, że
dσ x = −
dM y
z∗
Iy
(9)
zatem zależność (8) przyjmuje postać
τ xz =
1 dM y
b(z )I y dx
∫
A∗
z ∗dA
(10)
Wykorzystując relację (1.1.4), z której wynika, że siła poprzeczna nie może występować
samodzielnie, gdyż zawsze musi jej towarzyszyć moment zginający, czyli
dM y
= Tz
dx
(11)
zapisujemy zależność (10) w następującej, ostatecznej postaci:
τ xz =
TzS y∗
b(z )I y
(12)
zwanej wzorem ŻURAWSKIEGO, gdzie
S y∗ = ∫ ∗ z ∗dA
A
(13)
jest momentem statycznym części odciętej przekroju. We wzorze (12) opuściliśmy
nakreślenie nad naprężeniem stycznym pamiętając o tym, że określa ono naprężenie
średnie.
Zwrot naprężeń stycznych τ xz jest zawsze taki sam, jak zwrot siły poprzecznej Tz ,
natomiast ich znak przyjmujemy zgodnie z konwencją znakowania naprężeń stycznych
(por. 1.3.3). Zatem naprężenia te są dodatnie wtedy, gdy ich zwrot jest zgodny ze
dodatnim kierunkiem osi Oz układu odniesienia, przy równoczesnej zgodności zwrotu
normalnej zewnętrznej przekroju ze zwrotem osi Ox . W przeciwnym przypadku są one
ujemne.
Przykłady
Przykład 1. Wyznaczyć naprężenia styczne w przypadku przekroju jak na rys. P1.1.
Dane: Tz , b, h
Szukane: τ xz
Rys. P1.1
Rozwiązanie:
Krok 1. Obliczamy moment bezwładności przekroju
Iy =
bh3
12
Krok 2. Korzystając ze wzoru (13) obliczamy moment statyczny „części odciętej” przekroju prostą równoległą
do osi Oy i znajdującą się w odległości z od tej osi (rys. P1.2)
Rys. P1.2
Ponieważ w przypadku przekroju prostokątnego b(z ) = b , natomiast dA = bdz∗ , gdzie z∗ ∈ (z,h 2) , zatem
Sy∗ (z ) =
∫A
h2 ∗
z dz∗
z
z∗dA = b ∫
∗
=
( )
h2
b ∗2
z
2
z
=

b  h2
− z2 


2 4

Należy zauważyć, że w przypadku przekroju prostokątnego moment statyczny „części odciętej” możemy
wyznaczyć ze wzoru
Sy∗ = A∗zc∗
gdzie

h
A∗ = b − z 
2

oznacza pole powierzchni tej części przekroju, natomiast
zc∗ = z +
1h
 1h

 − z =  + z
22
2
2



współrzędną jej środka ciężkości. Zatem

 h
 b  h2
h
Sy∗ = b − z  + z  = 
− z2 


2
 2
 2 4

Krok 3. Korzystając ze wzoru ŻURAWSKIEGO (12) obliczamy naprężenia styczne w przekroju
Ponieważ siła poprzeczna Tz , moment bezwładności I y oraz szerokość przekroju b są w przypadku
przekroju prostokątnego stałe, zatem naprężenia styczne τ xz zależy jedynie od odległości z od centralnej
osi bezwładności Oy , czyli
τ xz =
Tz Sy∗
b Iy
=
 6T
b  h2
− z 2  = z3
3

 bh
bh 2  4

b
12
Tz

 h2

− z2 
 4



Z powyższego wzoru wynika, że rozkład naprężeń stycznych na wysokości przekroju opisuje parabola, przy
czym wartość maksymalną naprężenia te osiągają w punktach leżących na osi centralnej Oy przekroju
τ xz (0) = τ max =
3Tz
2bh
natomiast w skrajnych punktach przekroju naprężenia styczne są równe zeru

h
2
τ xz  ±  = 0

Wykres naprężeń stycznych przedstawia rys. P1.3
Rys. P1.3
Przykład 2. Wyznaczyć naprężenia styczne w przypadku przekroju jak na rys. P2.1.
Rys. P2.1
Dane: Tz , a
Szukane: τ xz
Rozwiązanie:
Krok 1. Wyznaczamy moment bezwładności przekroju
Z przykładu 3 w rozdziale 1.2 wynika, że środek ciężkości rozważanego przekroju znajduje się w punkcie
odległym o a od jego podstawy, natomiast moment bezwładności przekroju względem osi centralnej Oy
wynosi I y = 4a 4 .
Krok 2. Obliczamy moment statyczny „części odciętej” przekroju
Ponieważ rozważany przekrój składa się z dwóch prostokątów, w przypadku których rozkład naprężeń ma
kształt paraboli, zatem do wyznaczenia naprężeń wystarczy obliczyć moment statyczny „części odciętej” linią
leżącą na styku obu prostokątów (pokrywającą się z osią centralną Oy )
Sy∗ (z = 0 ) = a ⋅ 2a ⋅ a = 2a3
Krok 3. Korzystając ze wzoru Żurawskiego (12), który w rozważanym przypadku przyjmuje postać
τ xz (z ) =
Tz Sy∗
=
b(z )Iy
Tz 2a3
b(z ) 4a
4
=
Tz
2b(z )a
gdzie
b(z > 0 ) = a,
b(z < 0 ) = 4a
obliczamy naprężenia styczne w punktach skrajnych przekroju
τ xz (2a ) = 0, τ xz (− a ) = 0
oraz w punktach leżących na styku obu prostokątów
( )
τ xz 0+ = τ max =
( )
τ xz 0− =
Tz
Tz
T
=
= z2
2b(z )a 2 ⋅ a ⋅ a 2a
Tz
Tz
T
=
= z
2b(z )a 2 ⋅ 4a ⋅ a 8 a2
Wykres naprężeń stycznych przedstawia rys. P2.2
Rys. P2.2
Z wykresu tego wynika, że na styku obu prostokątów (w miejscu skokowej zmiany szerokości przekroju)
występuje nieciągłość (skok) funkcji τ xz (z ) , przy czym
( )
( )
Tz
( )
( )
τ xz 0 +
b 0−
4a
2a2
=
=
=
=4
−
+
Tz
a
b0
τ xz 0
8 a2
W rzeczywistości, w tego typu miejscach rozkład naprężeń stycznych jest bardziej złożony; występuje w nich
koncentracja (miejscowe zwiększenie) naprężeń. W celu jej uniknięcia w miejscach łączenia elementów
przekroju o różnej szerokości stosuje się odpowiednie zaokrąglenia (np. w profilach walcowanych).